A hybrid approach to compute convection-dominated mass transfer at rising bubbles
Andre Weiner, a.weiner@tu-bs.de
Prof. Dr. rer. nat. Dieter Bothe, bothe@mma.tu-darmstadt.de
Slides available at: andreweiner.github.io/reveal.js/gofun2020.html

Gas-liquid reactors

micro reactor
size: millimeter
source: SPP 1740
prediction of
- mass transfer
- enhancement
- mixing
- conversion
- selectivity
- yield
- ...

bubble column reactor
size: meter
source: R. M. Raimundo, ENI
High Péclet number problem

U. D. Kück, M. Schlüter, N. Räbiger:
Analyse des grenzschichtnahen Stofftransports an frei aufsteigenden Gasblasen (2009)
Specimen calculation
$d_b=1~mm$ water/oxygen at room temperature
- $Pe = Sc\ Re = \nu_l / D_{O_2} \cdot U_b d_b/\nu_l \approx 10^5 $
- $$ Re\approx 250;\quad \delta_h/d_b \propto Re^{-1/2};\quad\delta_h\approx 45~\mu m $$
- $$ Sc\approx 500;\quad \delta_c/\delta_h \propto Sc^{-1/2};\quad\delta_c\approx 2.5~\mu m $$
$\delta_h/\delta_c$ typically 10 ... 100
feasible simulations up to $Pe\approx 1000$ (3D, HPC)
Basic idea
mitigate complexity by decoupling two-phase flow and mass transfer
Outline
- Hybrid approach overview
- Volume-of-Fluid simulations
Shape parametrization and approximation
learn more- Velocity at the interface
- Single-phase flow dynamics
- Single-phase mass transfer
- Summary and outlook
Hybrid approach overview
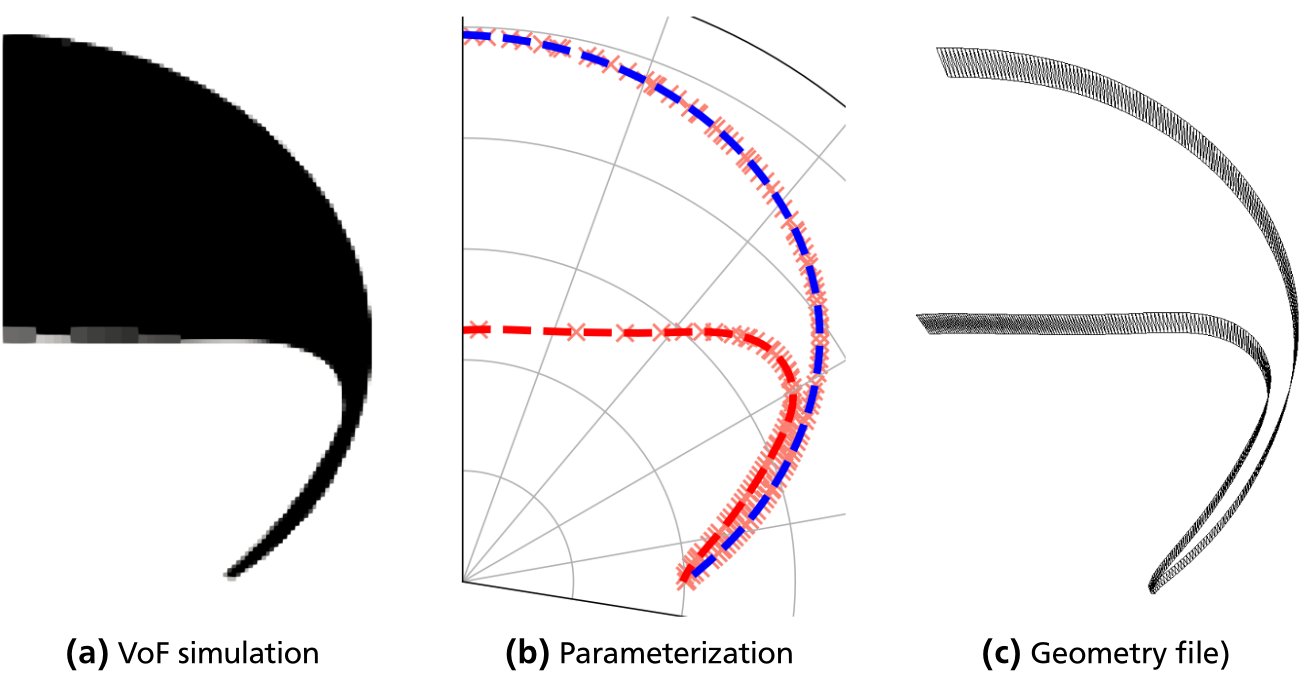
Hybrid approach overview
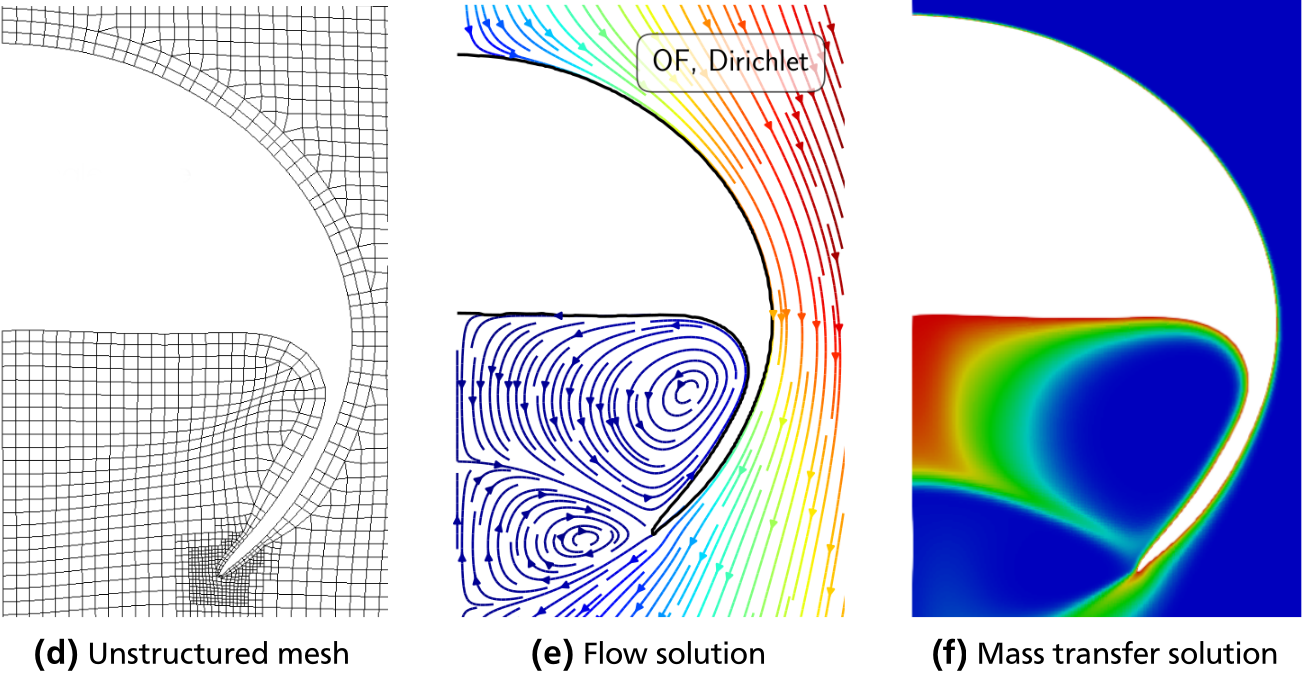
Volume-of-Fluid simulations
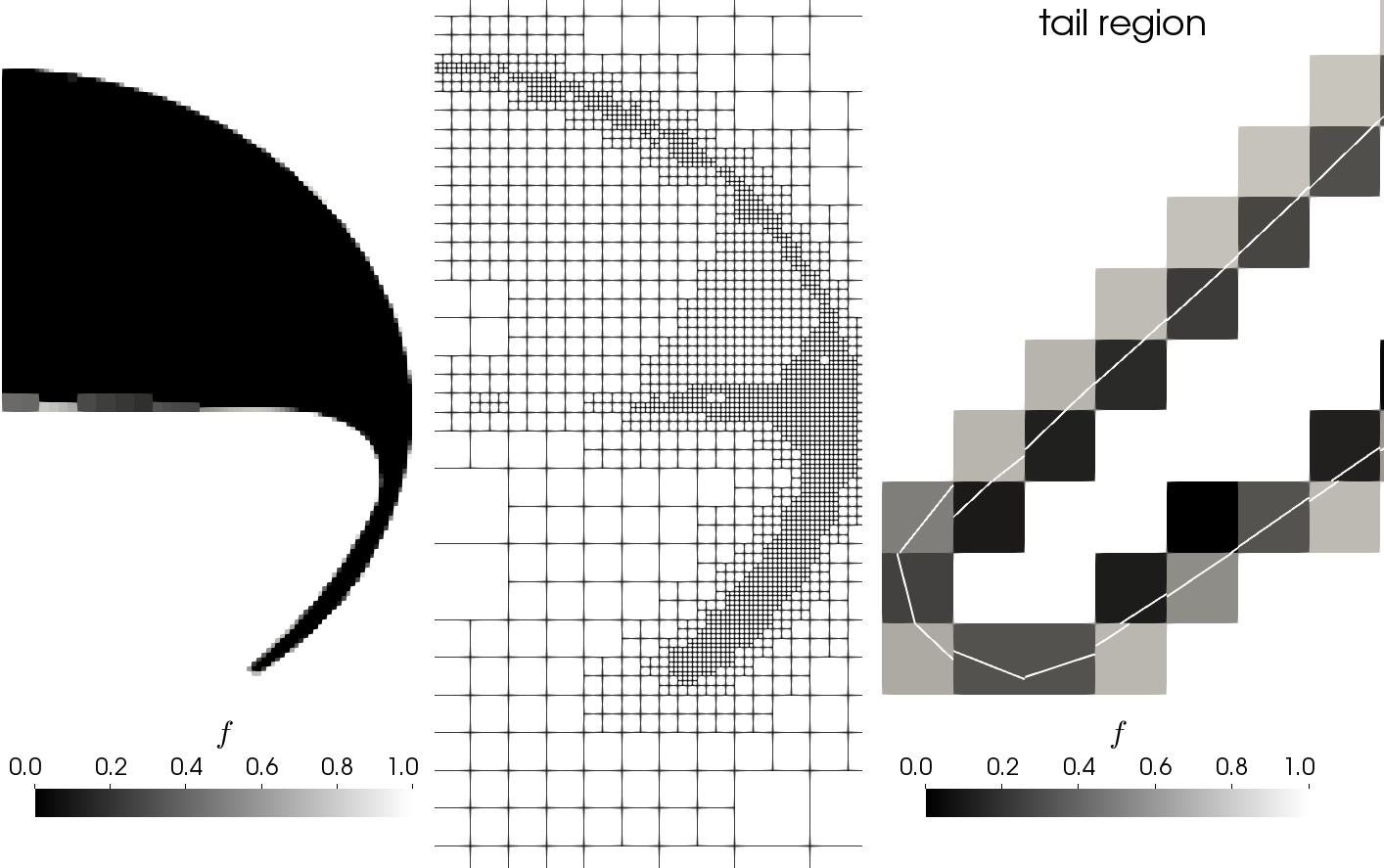
Keywords: Basilisk, geometrical advection with PLIC recontruction, adaptive mesh refinement, curvature computation based on height functions, learn more (Github).
Characteristic bubble shapes
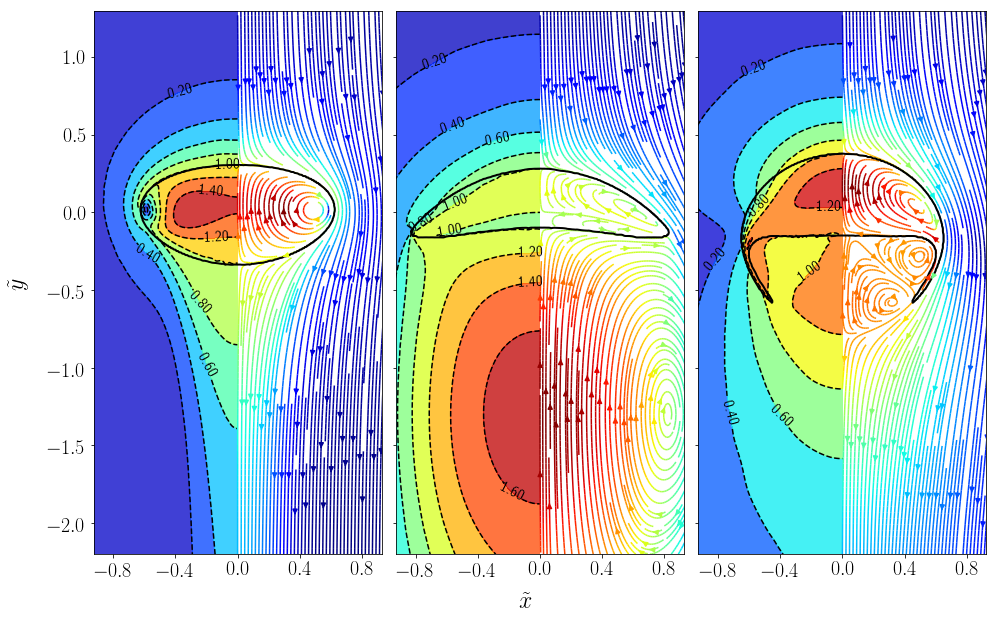
From left to right: ellipsoidal, spherical cap, dimpled ellipsoidal.
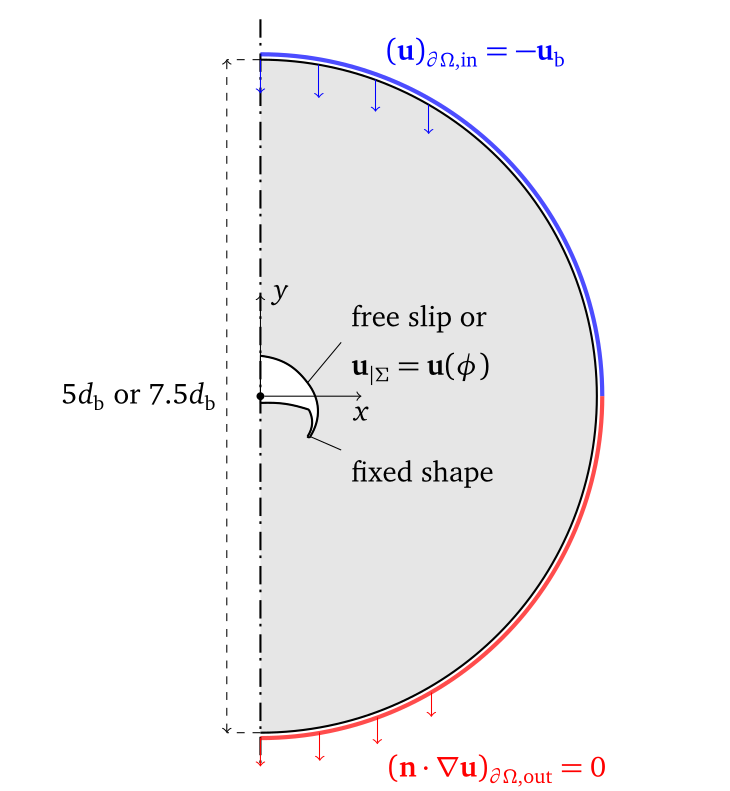
Velocity at the interface
- mathematical framework: sharp interface model
- mass conservation at the interface: $\quad u_{\bot}^{gas} = u_{\bot}^{liq} $
- steady shape: $\quad u_{\bot}^{gas} = u_{\bot}^{liq} = 0$
- assumption: $\quad u_{\parallel}^{gas} = u_{\parallel}^{liq}$
How to model $u_{\parallel}^{liq}$ in single-phase simulations?
Parametrization and machine learning
- extract velocity vector from two-phase simulations
- create ML model based on extracted data (here: multilayer perceptron, PyTorch)
- export model to torch script (.pt)
-
- star-shaped: $u_\parallel = u_\parallel (\varphi)$ with polar angle $\varphi$
- complex shapes: $u_\parallel = u_\parallel (s)$ with arc length $s$
Final model
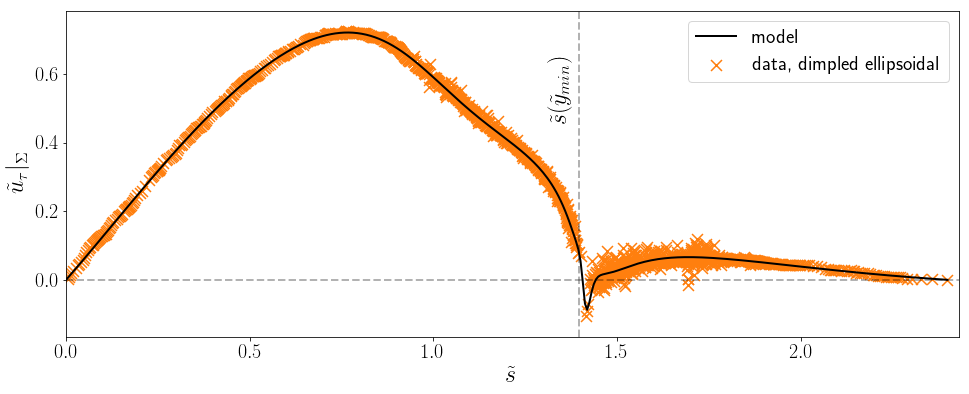
Learn more: publication, Jupyter notebooks
Single-phase flow dynamics
Implementation in OpenFOAM
bubbleSurfaceVelocitySimpleFvPatchVectorField.H
class bubbleSurfaceVelocitySimpleFvPatchVectorField
:
public fixedValueFvPatchVectorField
{
// Private data
...
//- name of the PyTorch model
word model_name_;
//- PyTorch model
torch::jit::script::Module pyTorch_model_;
...
Implementation in OpenFOAM
bubbleSurfaceVelocitySimpleFvPatchVectorField.C
Foam::bubbleSurfaceVelocitySimpleFvPatchVectorField::
bubbleSurfaceVelocitySimpleFvPatchVectorField
(
const fvPatch& p,
const DimensionedField<vector, volMesh>& iF,
const dictionary& dict
)
:
fixedValueFvPatchField<vector>(p, iF, dict, false),
...
model_name_(dict.lookupOrDefault<word>("model", "velocity_model.pt"))
{
pyTorch_model_ = torch::jit::load(model_name_);
}
Implementation in OpenFOAM
bubbleSurfaceVelocitySimpleFvPatchVectorField.C
void Foam::bubbleSurfaceVelocitySimpleFvPatchVectorField::updateCoeffs()
{
...
// run forward pass to compute tangential velocity
std::vector<torch::jit::IValue> modelFeatures{phiTensor};
torch::Tensor uTensor = pyTorch_model_.forward(modelFeatures).toTensor();
auto uAccessor = uTensor.accessor<double,1>();
vectorField surfaceVelocity(Cf.size(), Zero);
forAll(surfaceVelocity, faceI)
{
surfaceVelocity[faceI] = tau[faceI] * uAccessor[faceI];
}
...
Boundary condition
bubble patch in 0/U
bubble
{
type bubbleSurfaceVelocitySimple;
origin (0 0 0);
axis (0 1 0);
normal (0 0 -1);
model "bhaga_02_u_tau.pt";
}
Meshes

Wedge mesh creation: blockMesh, snappyHexMesh, extrudeMesh, collapseEdges
Comparison to free slip
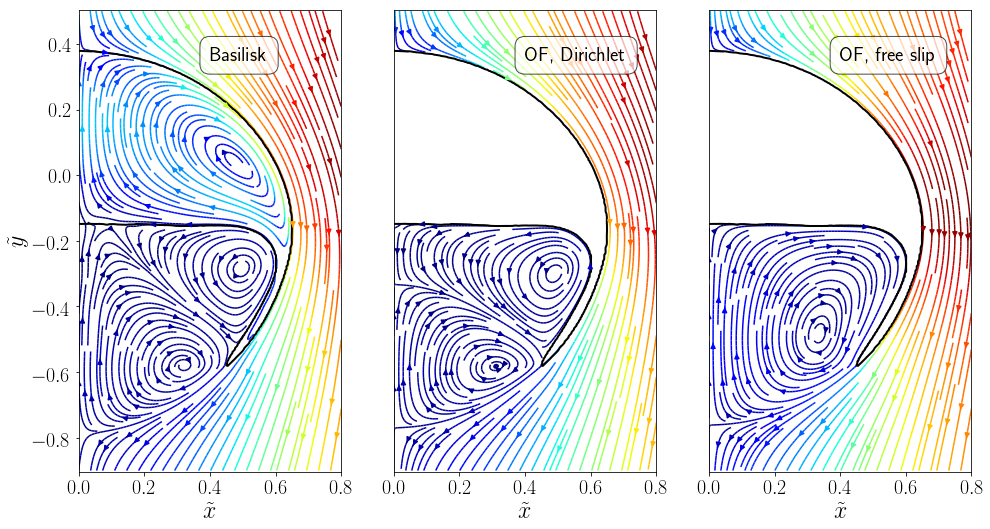
OpenFoam test cases on Github
Jupyter notebooks for post-processing on Github
Single-phase mass transfer
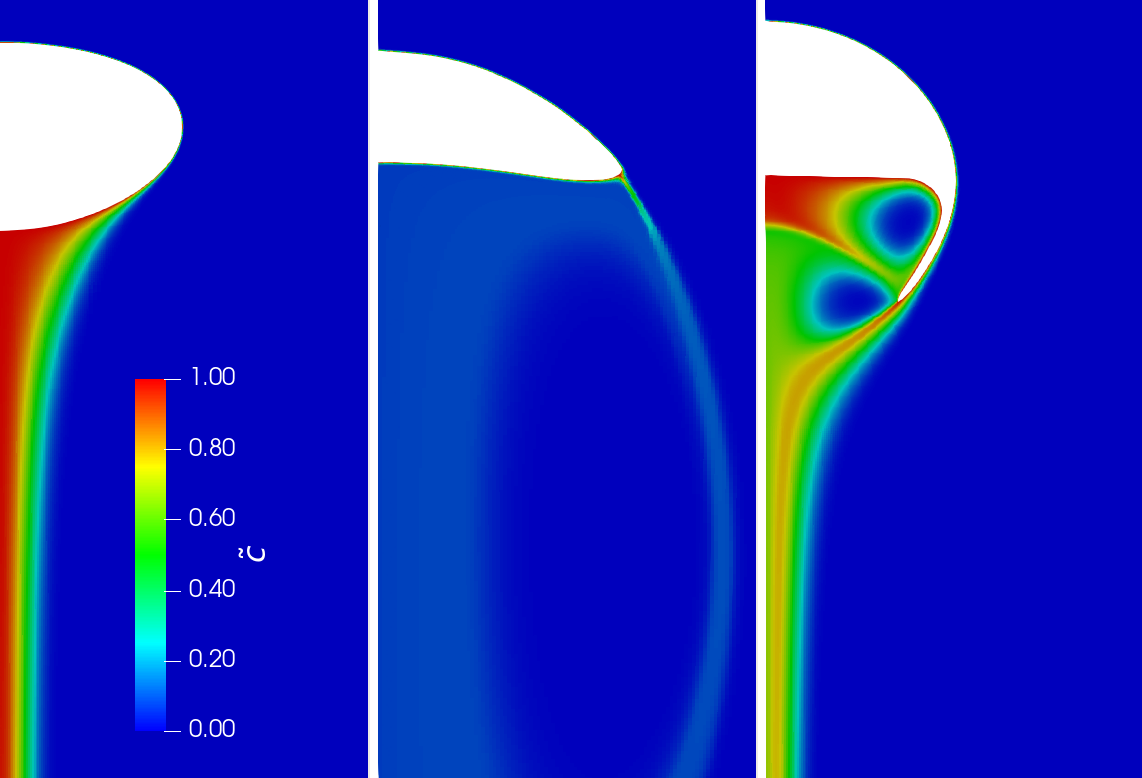
Physisorption $ A^{gas} \rightarrow A^{liq}$
Global Sherwood number
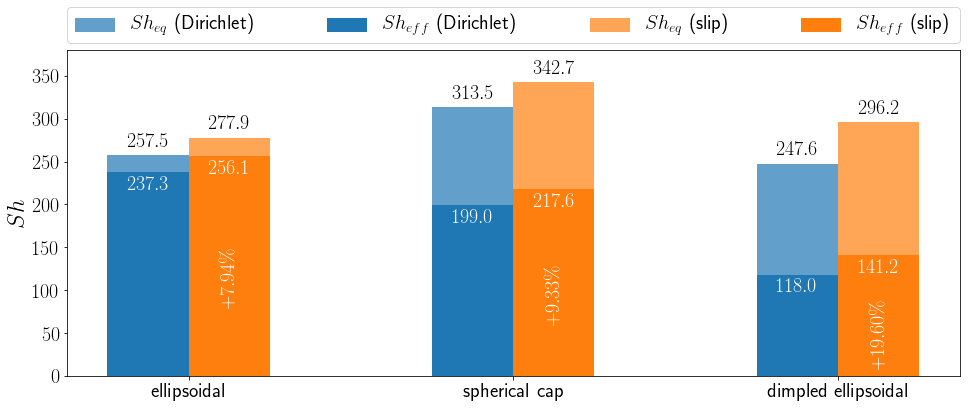
Comparison of global Sherwood number computed with Dirichlet and slip boundary condition.
Summary
- hybrid approach: decoupling of two-phase flow and species transfer problem
- computationally efficient: minutes to hours on a single core (end to end)
- data-driven: machine learning maps information from two-phase to single-phase simulations
Outlook
assessment for dynamic interfaces
THE END
Thank you for your attention!
Get in touch:
- a.weiner@tu-bs.de
- ml-cfd.com
- github.com/AndreWeiner
- From May 2020: Flow modeling and control, ISM, TU Braunschweig

Mesh tail region
