Closed-loop active flow control

motivation for closed-loop active flow control

• adaptation to more than one design point
• more efficient than open-loop control

How to find the control law?

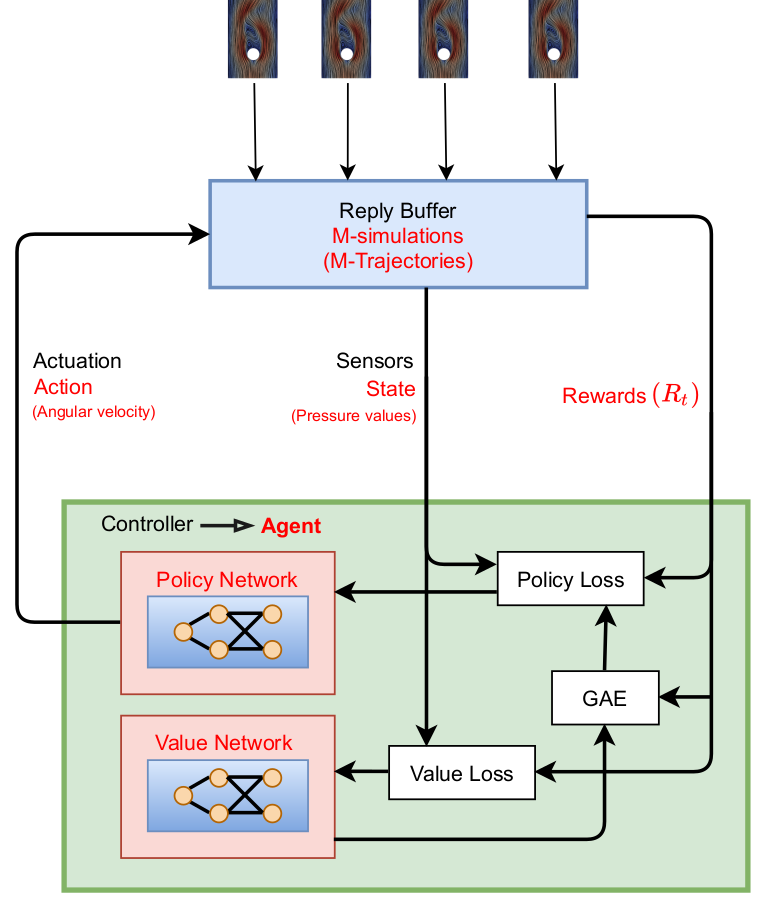
Proximal policy optimization (PPO) workflow (GAE - generalized advantage estimate).

Training cost DrivAer model

• $8$ hours/simulation (2000 MPI ranks)
• $10$ parallel simulations
• $3$ episodes/day
• $60$ days/training (180 episodes)
• $60\times 24\times 10\times 2000 \approx 30\times 10^6 $ core hours

CFD environments are expensive!

Optimal sensor placement

Tom Krogmann, Github, 10.5281/zenodo.7636959

Challenge with optimal sensor placement and flow control:
actuation changes the dynamical system

Idea: combined sensor placement and flow control optimization via attention layer

$$\mathbf{f} = \mathbf{W}_2\mathrm{tanh}(\mathbf{W}_1\mathbf{x}_{in})$$

$\mathbf{W}_1\in \mathbb{R}^{N_b\times N_{in}}$, $\mathbf{W}_2\in \mathbb{R}^{N_{in} \times N_b}$, $N_b < N_{in}$

$$ \kappa_i = \mathrm{exp}(f_i)/\sum_i\mathrm{exp}(f_i)$$

$\kappa_i$ - attention weight of sensor $i$

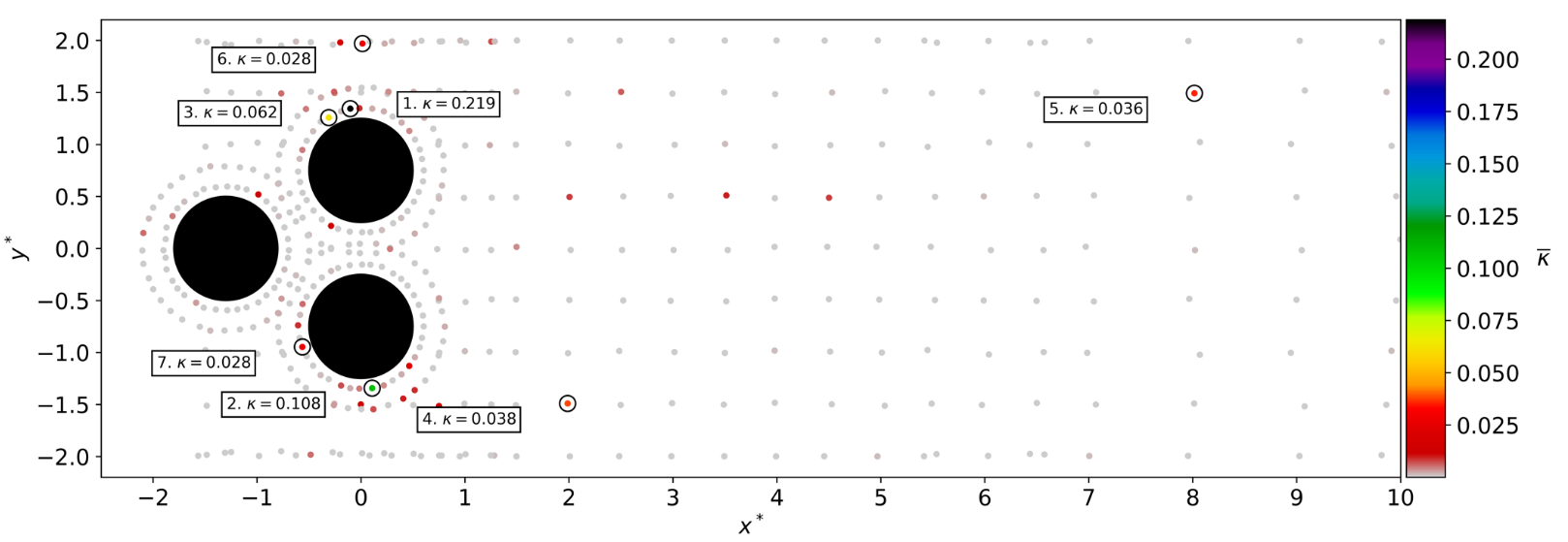
Time-averaged attention weights $\bar{\kappa}$.

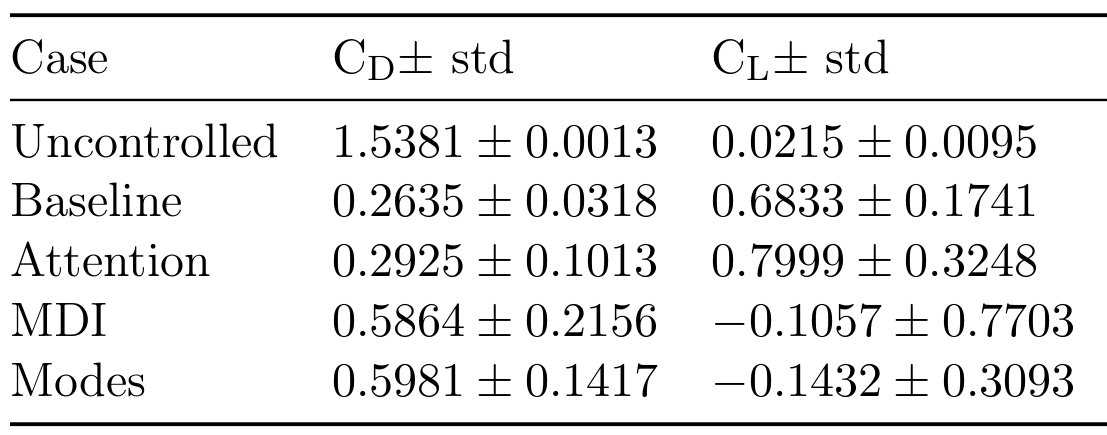
Results obtained with top 7 sensors (MDI - mean decrease of impurity, modes - QR column pivoting).

Model-based PPO

Janis Geise, Github, 10.5281/zenodo.7642927

Idea: replace CFD with model(s) in some episodes

for e in episodes:
    if models_reliable():
        sample_trajectories_from_models()
    else:
        sample_trajectories_from_simulation()
        update_models()
    update_policy()
					

Based on Model Ensemble TRPO.

When are the models reliable?

1. evaluate policy for every model
2. compare to previous policy loss
3. switch if loss did not decrease for
   at least $50\%$ of the models

How to sample from the ensemble?

1. pick initial sequence from CFD
2. fill buffer with trajectories
   1. select random model
   2. sample action
   3. predict next state

Recipe to create env. models:

• input/output normalization
• fully-connected, feed-forward
• time delays (~30)
• layer normalization
• batch training (size ~100)
• learning rate decay (on plateau)
• "early stopping"

Cylinder benchmark case; $Re=100$.

control objective

$$r = c_{d,ref} - (c_d + 0.1|c_l|)$$

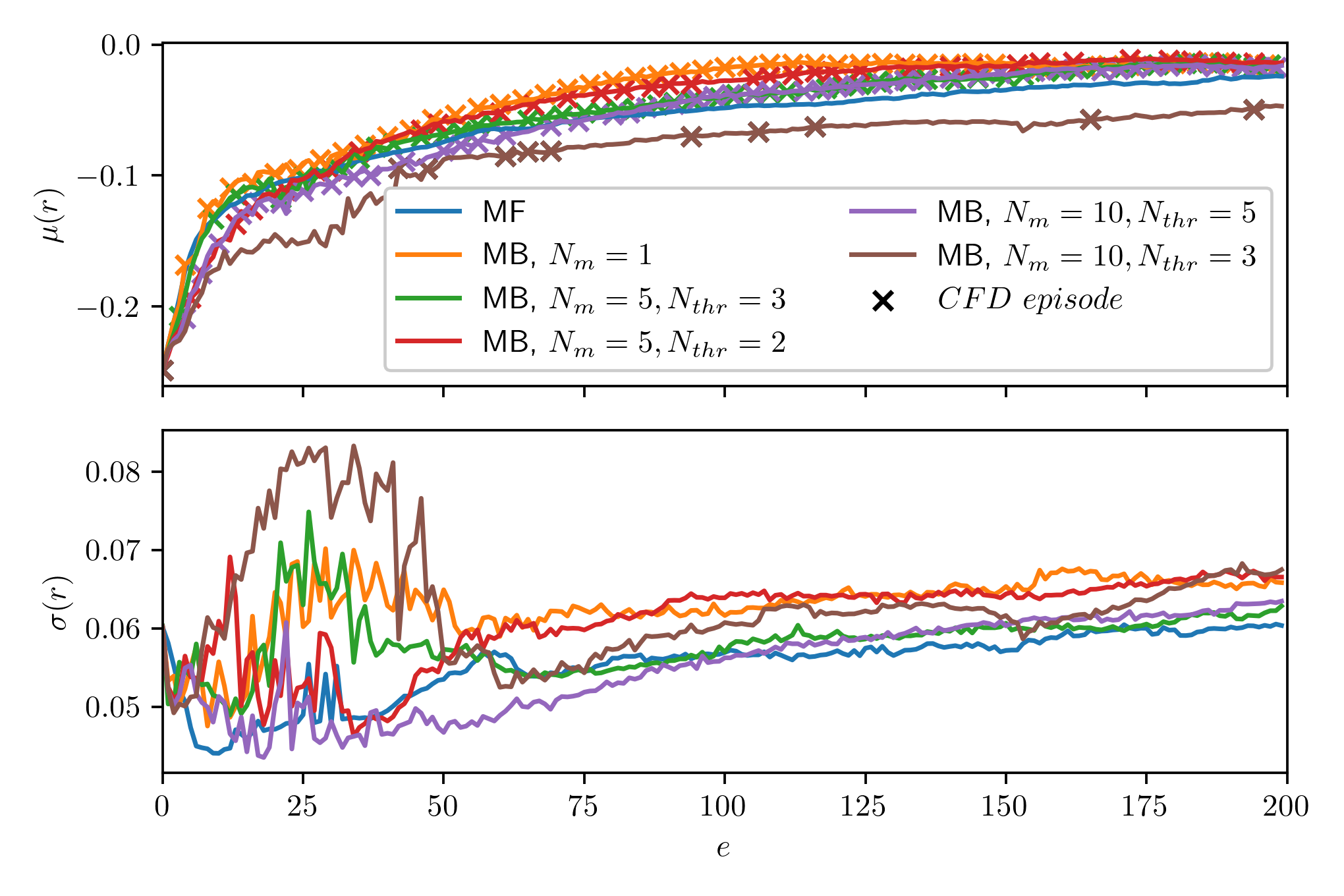
Rewards over episodes; mean/std. over 10 trajectories and 5 seeds; markers indicate CFD episodes.

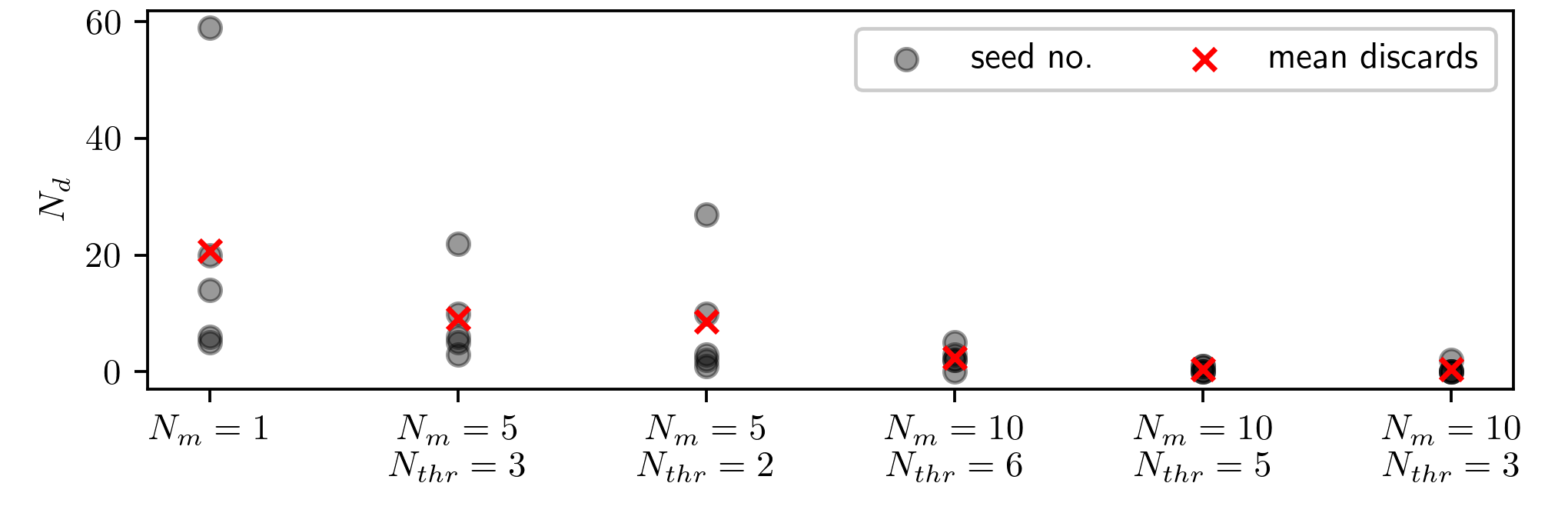
Number of discarded trajectories $N_r$ for various ensembles.

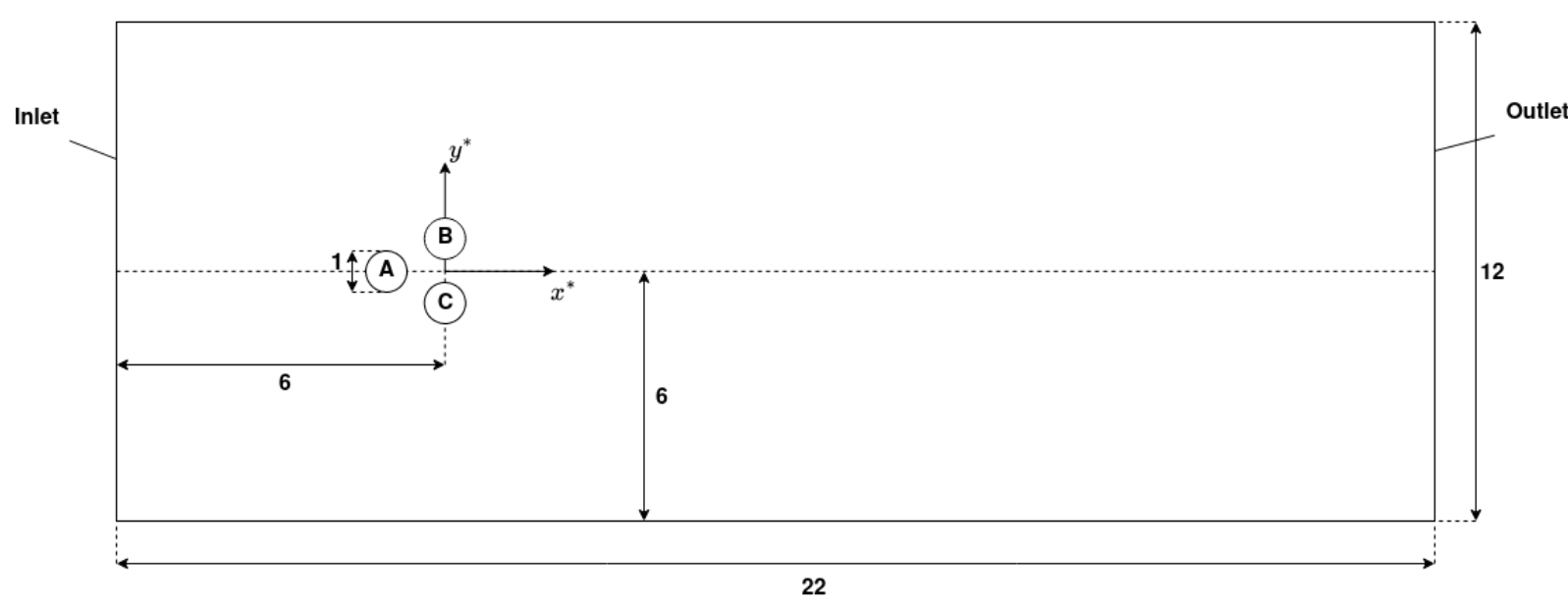
Pinball benchmark case; $Re=100$.

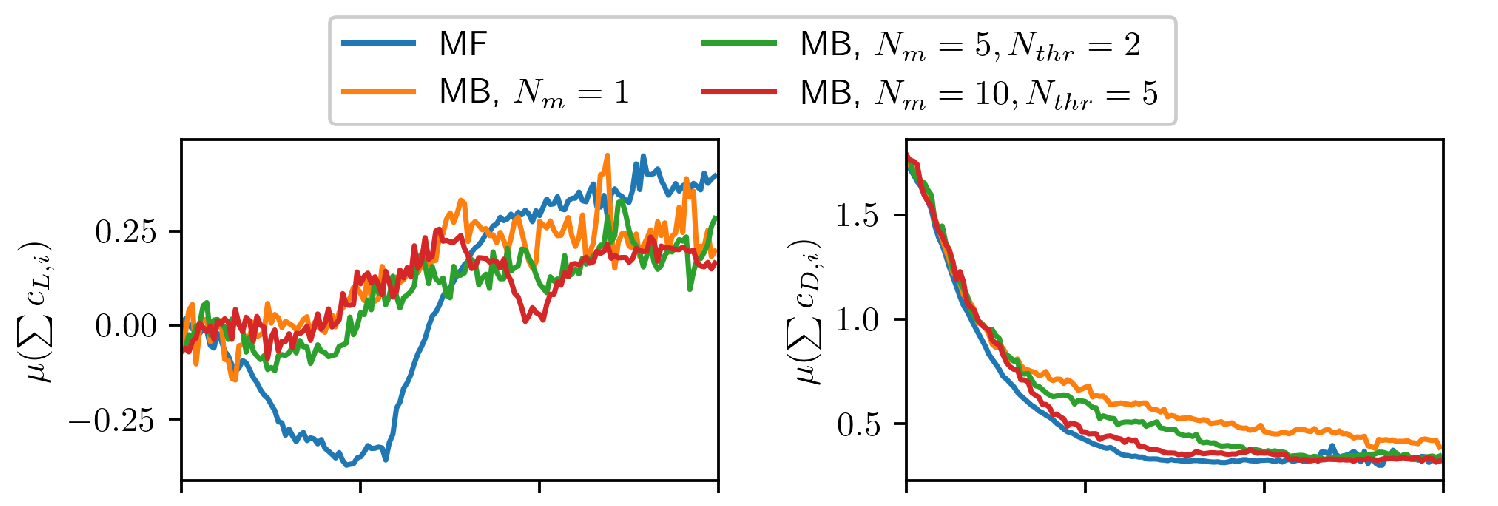
Mean drag/lift over episodes.

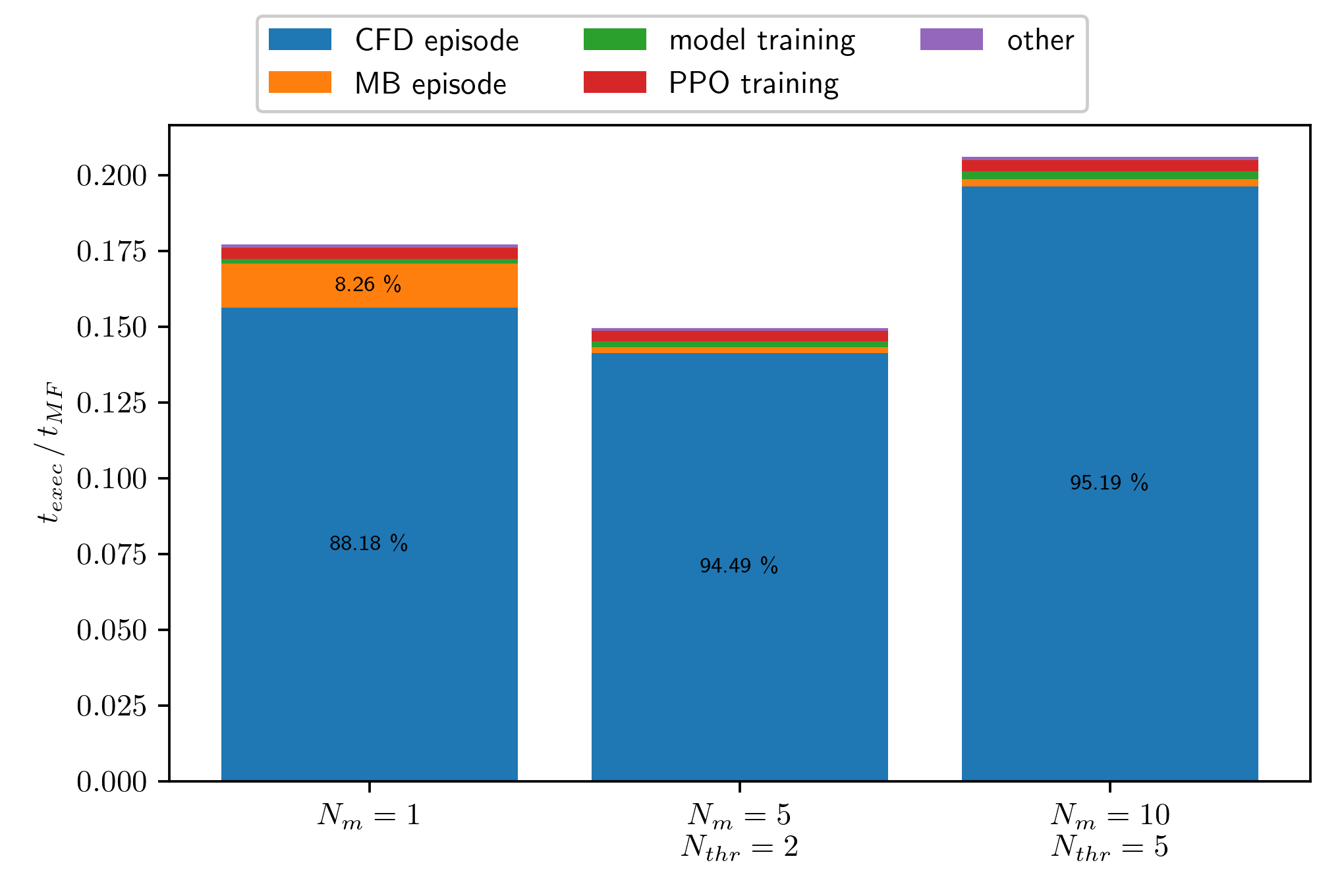
Execution time $t_{exec}$ for various ensembles normalized by model-free training time $t_{MF}$.

Evaluation of final policy.

THE END

Thank you for you attention!