An optimized dynamic mode decomposition for flow analysis
Andre Weiner, Janis Geise, Richard Semaan
TU Dresden, Chair of Fluid
Mechanics
A simple 1D test signal.
First component - jumping rope.
Second component - see-saw.
Third component - flipping wave.
Superposition yields the original signal.
Outline
- dynamic mode decomposition
- optimized DMD and benchmarks
- example: surface-mounted cube
Dynamic Mode Decomposition
$\mathbf{x}_n = \mathbf{x}(t=n\Delta t)$
$\mathbf{x}_{n+1} = \mathbf{x}(t=(n+1)\Delta t)$
$\quad\mathbf{x}_{n+1} = \mathbf{Ax}_n $
- $\mathbf{x}\in \mathbb{R}^M$ - state vector
- $\mathbf{A}\in \mathbb{R}^{M\times M}$ - linear operator
Least-squares definition of $\mathbf{A}$
$$ \underbrace{[\mathbf{x}_2, ..., \mathbf{x}_N]}_{\mathbf{Y}} = A \underbrace{[\mathbf{x}_1, ..., \mathbf{x}_{N-1}]}_{\mathbf{X}} $$
$$ \underset{\mathbf{A}}{\mathrm{argmin}} ||\mathbf{Y}-\mathbf{AX}||_F = \mathbf{YX}^\dagger $$
$^\dagger$ denotes the pseudo inverse
Useful properties of the eigendecomposition $$ \mathbf{A} = \mathbf{\Phi\Lambda\Phi}^{-1} $$
$$ \mathbf{x}_2 = \mathbf{Ax}_1 = \mathbf{\Phi\Lambda\Phi}^{-1} \mathbf{x}_1 $$
$$ \mathbf{x}_3 = \mathbf{AAx}_1 = \mathbf{\Phi\Lambda\Phi}^{-1}\mathbf{\Phi\Lambda\Phi}^{-1} \mathbf{x}_1 = \mathbf{\Phi\Lambda}^{2}\mathbf{\Phi}^{-1} \mathbf{x}_1 $$
$$ \mathbf{x}_n = \mathbf{\Phi\Lambda}^{n-1}\mathbf{\Phi}^{-1} \mathbf{x}_1 $$ Only the $\mathbf{\Lambda}$ term encodes time dependency!
Dealing with large snapshots - DMD:
- $\mathbf{X} = \mathbf{U\Sigma V}^T$
- $\tilde{\mathbf{A}} = \mathbf{U}_r^T \mathbf{AU}_r = \mathbf{U}_r^T \mathbf{YX}^\dagger\mathbf{U}_r$, $\quad \tilde{\mathbf{A}} \in \mathbb{R}^{r\times r}$
- $\tilde{\mathbf{A}} = \mathbf{U}_r^T\mathbf{Y}\mathbf{V}_r\mathbf{\Sigma}_r^{-1}\mathbf{U}_r^T\mathbf{U}_r = \mathbf{U}_r^T\mathbf{Y}\mathbf{V}_r\mathbf{\Sigma}_r^{-1}$
- $\tilde{\mathbf{A}} =\mathbf{W\Lambda}_r\mathbf{W}^{-1}$, $\quad \mathbf{W}, \mathbf{\Lambda}_r \in \mathbb{C}^{r\times r}$
- $\mathbf{\Phi}_r = \mathbf{U}_r\mathbf{W}$
Issues with the standard DMD:
- poor reconstruction accuracy
- data overfitting
- sensitive w.r.t. noise/nonlinearity
- sensitive w.r.t. truncation ($r$)
Optimized DMD
Reconstruction of a single snapshot: $$ \mathbf{x}_n \approx \mathbf{\Phi}_r\mathbf{\Lambda}_r^{n-1}\mathbf{b}_r $$ with $\mathbf{b}_r = \mathbf{\Phi}^{-1} \mathbf{x}_1$
reconstruction of the full dataset
$$ \underbrace{ \begin{bmatrix} x_{11} & \ldots & x_{1N}\\ \vdots & \ddots & \vdots\\ x_{M1} & \ldots & x_{MN} \end{bmatrix} }_{\mathbf{M}} \approx \underbrace{ \begin{bmatrix} \phi_{11} & \ldots & \phi_{1r}\\ \vdots & \ddots & \vdots\\ \phi_{M1} & \ldots & \phi_{Mr} \end{bmatrix} }_{\mathbf{\Phi}_r} \underbrace{ \begin{bmatrix} b_1& & \\ & \ddots & \\ & & b_r \end{bmatrix} }_{\mathbf{D_b}} \underbrace{ \begin{bmatrix} \lambda_{1}^0 & \ldots & \lambda_{1}^{N-1}\\ \vdots & & \vdots\\ \lambda_r^0 & \ldots & \lambda_r^{N-1} \end{bmatrix} }_{\mathbf{V_\lambda}} $$
with $\mathbf{b}_r = \mathbf{\Phi}_r^{-1}\mathbf{x}_1$, $M$ - length of $\mathbf{x}$, $N$ - number of snapshots, $r$ - truncation rank
Operator definition in the optimized DMD:
$\mathbf{M} = \left[ \mathbf{x}_1, \ldots, \mathbf{x}_{N} \right]^T\approx \mathbf{\Phi}_r\mathbf{D_b}\mathbf{V}_{\mathbf{\lambda}_r}$$$ \underset{\mathbf{\lambda}_r,\mathbf{\Phi}_r,\mathbf{b}_r}{\mathrm{argmin}}\left|\left| \mathbf{M}-\mathbf{\Phi}_r\mathbf{D_b}\mathbf{V}_{\mathbf{\lambda}_r} \right|\right|_F $$
$\rightarrow$ "optDMD" problem is nonlinear and non-convex
idea: borrow techniques from ML/DL
- stochastic gradient descent
- automatic differentiation
- train-validation-split
- early stopping
$\rightarrow$ refer to 10.48550/arXiv.2312.12928 for details
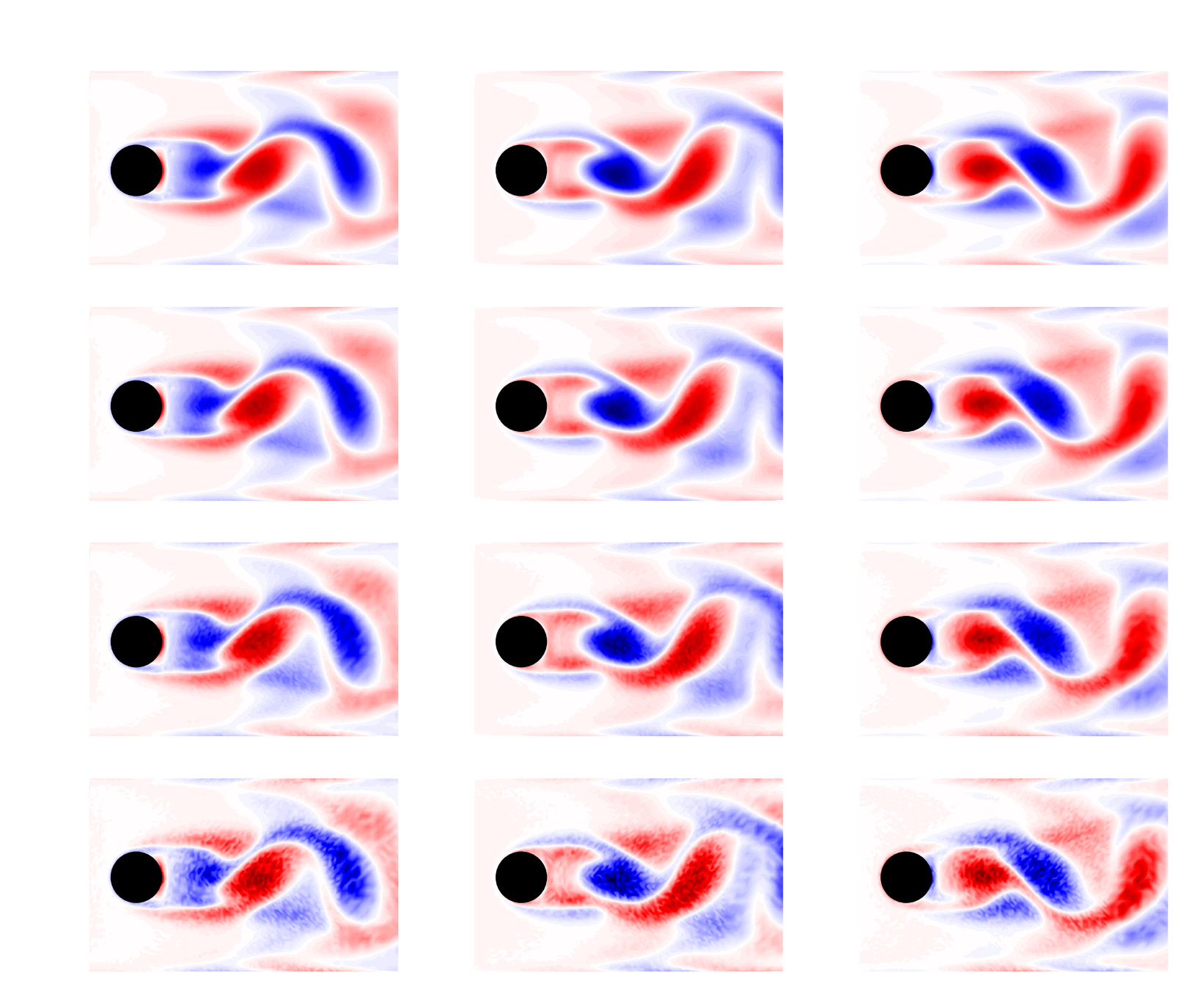
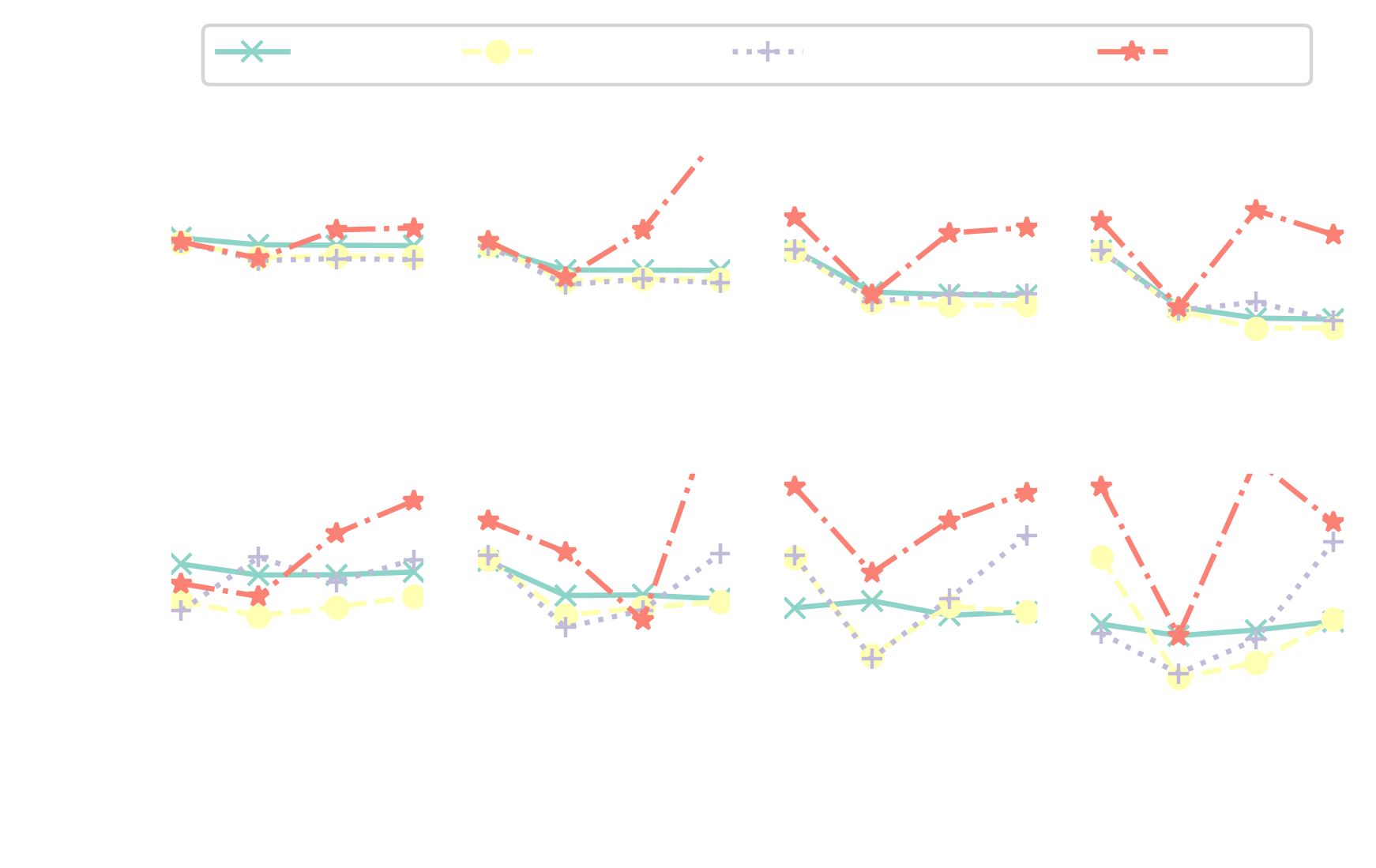
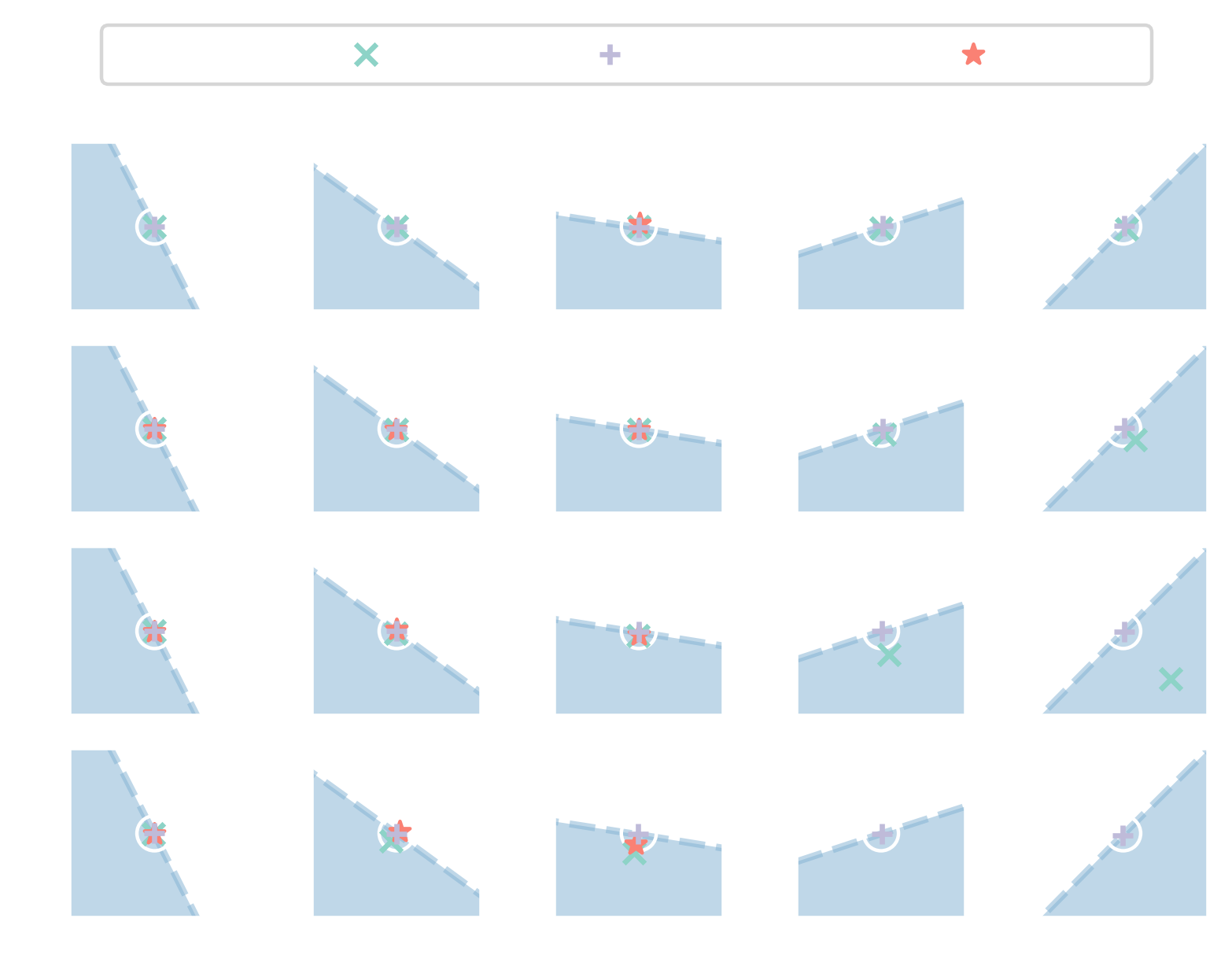
Surface-mounted cube
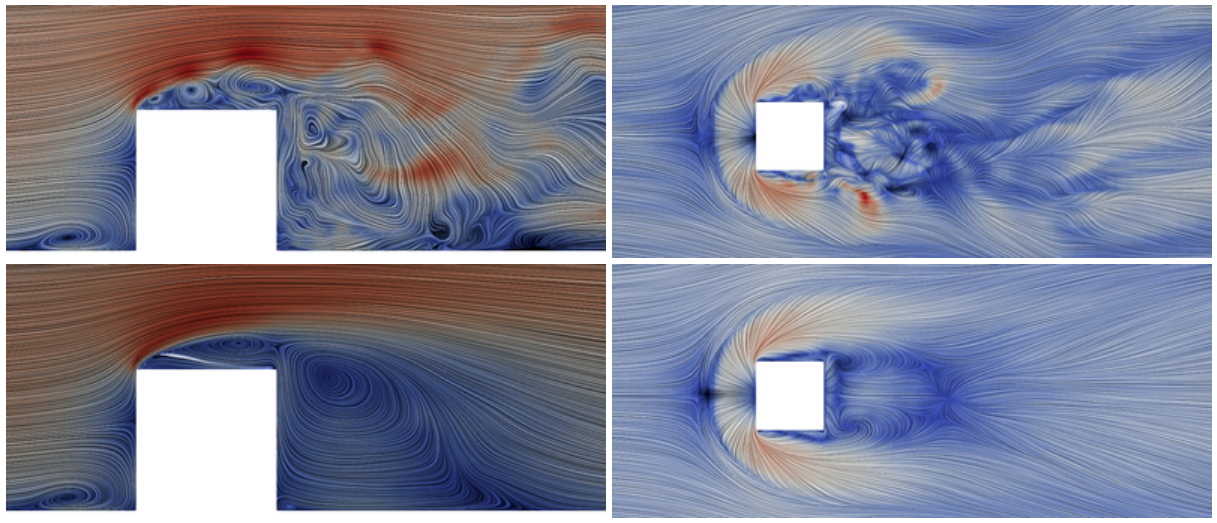
Surface-mounted cube at $Re_h = 40000$; image source
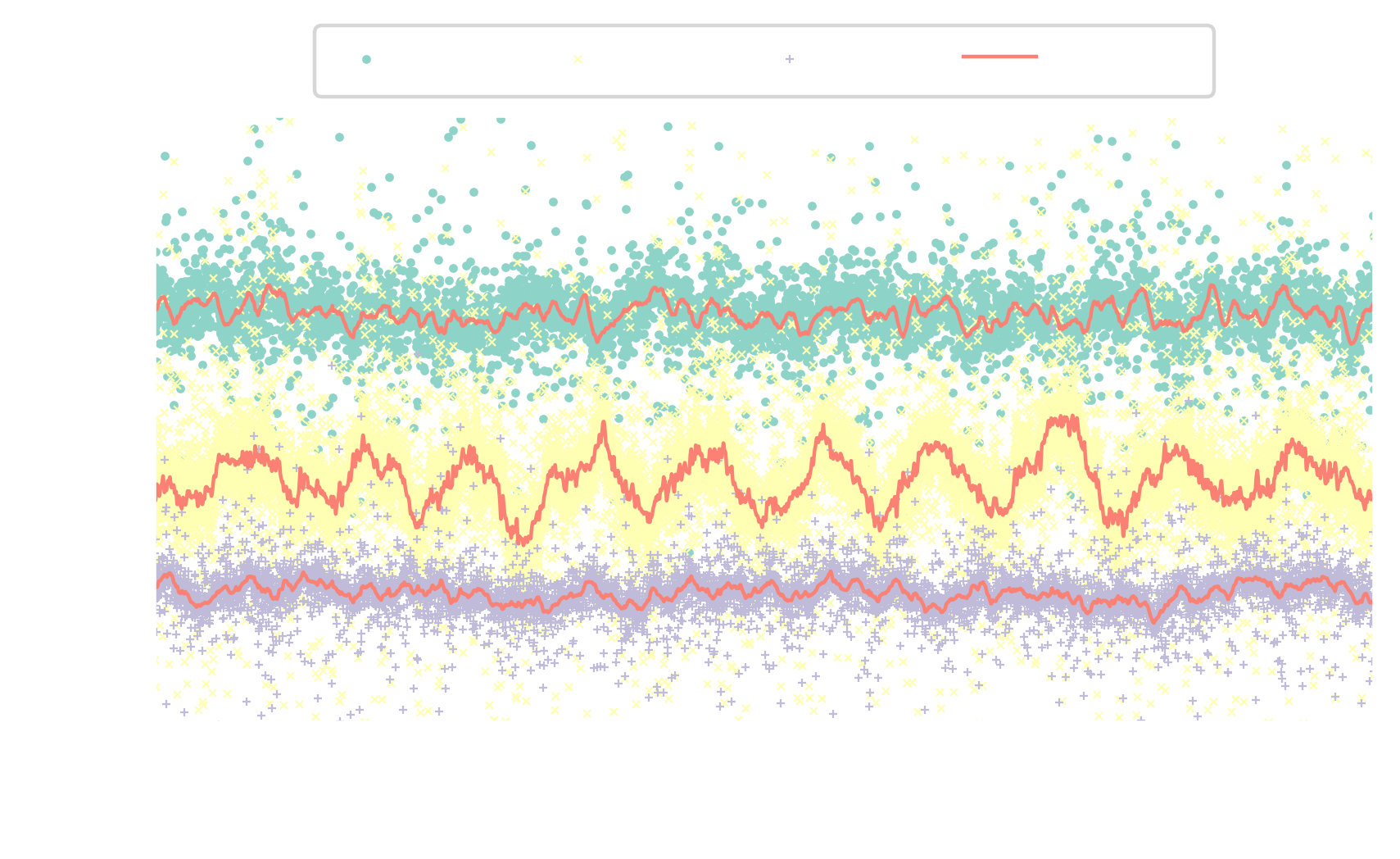
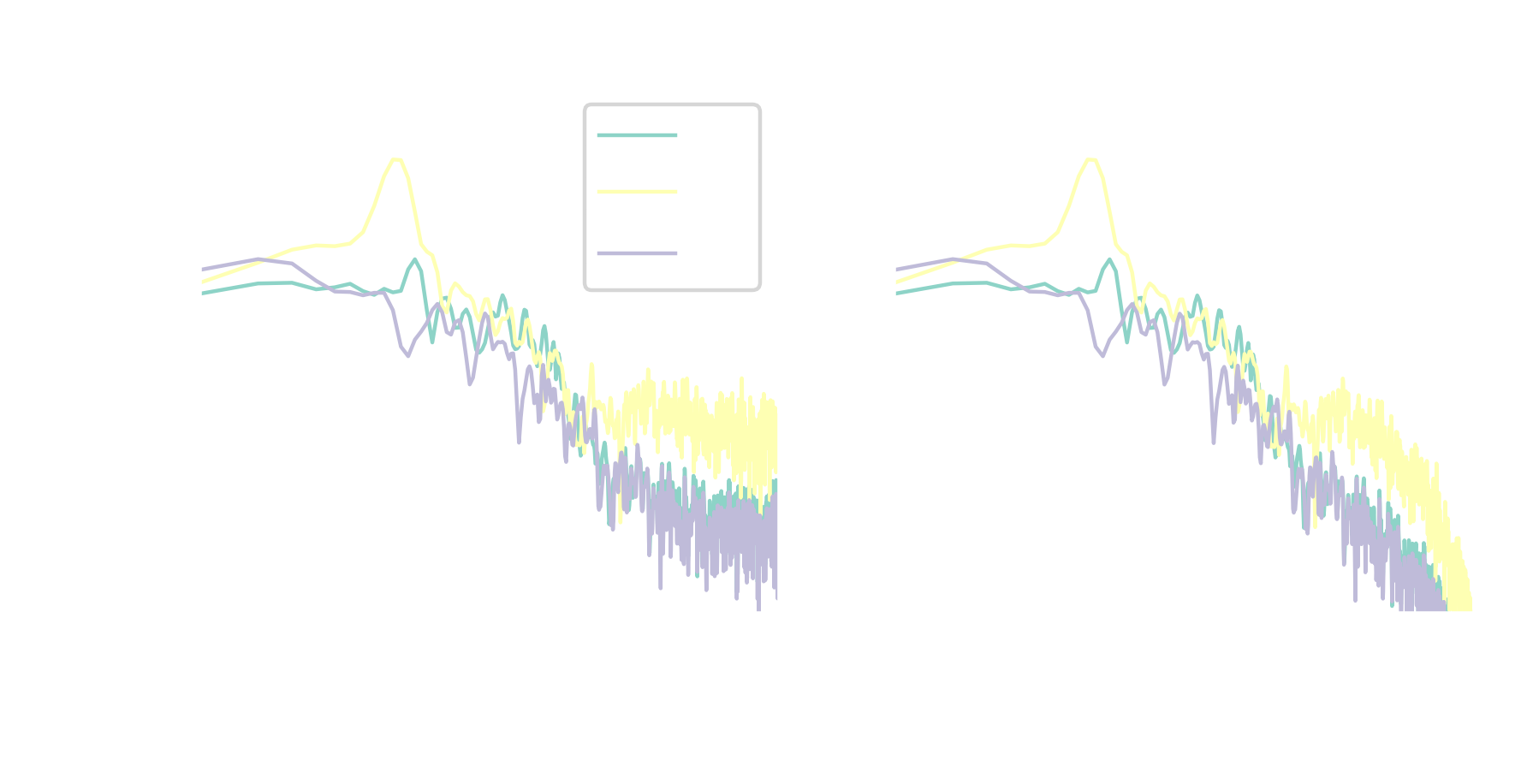
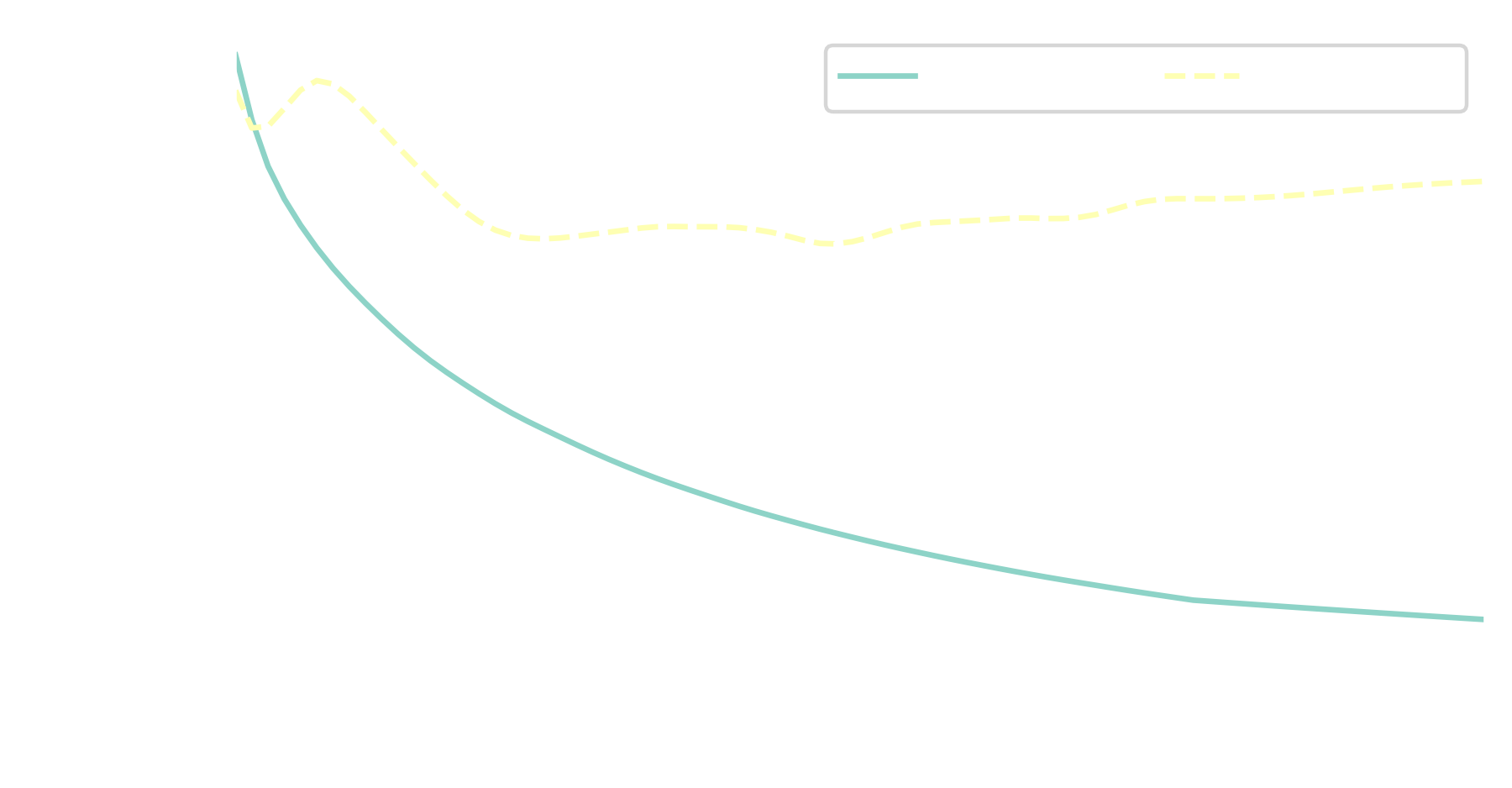
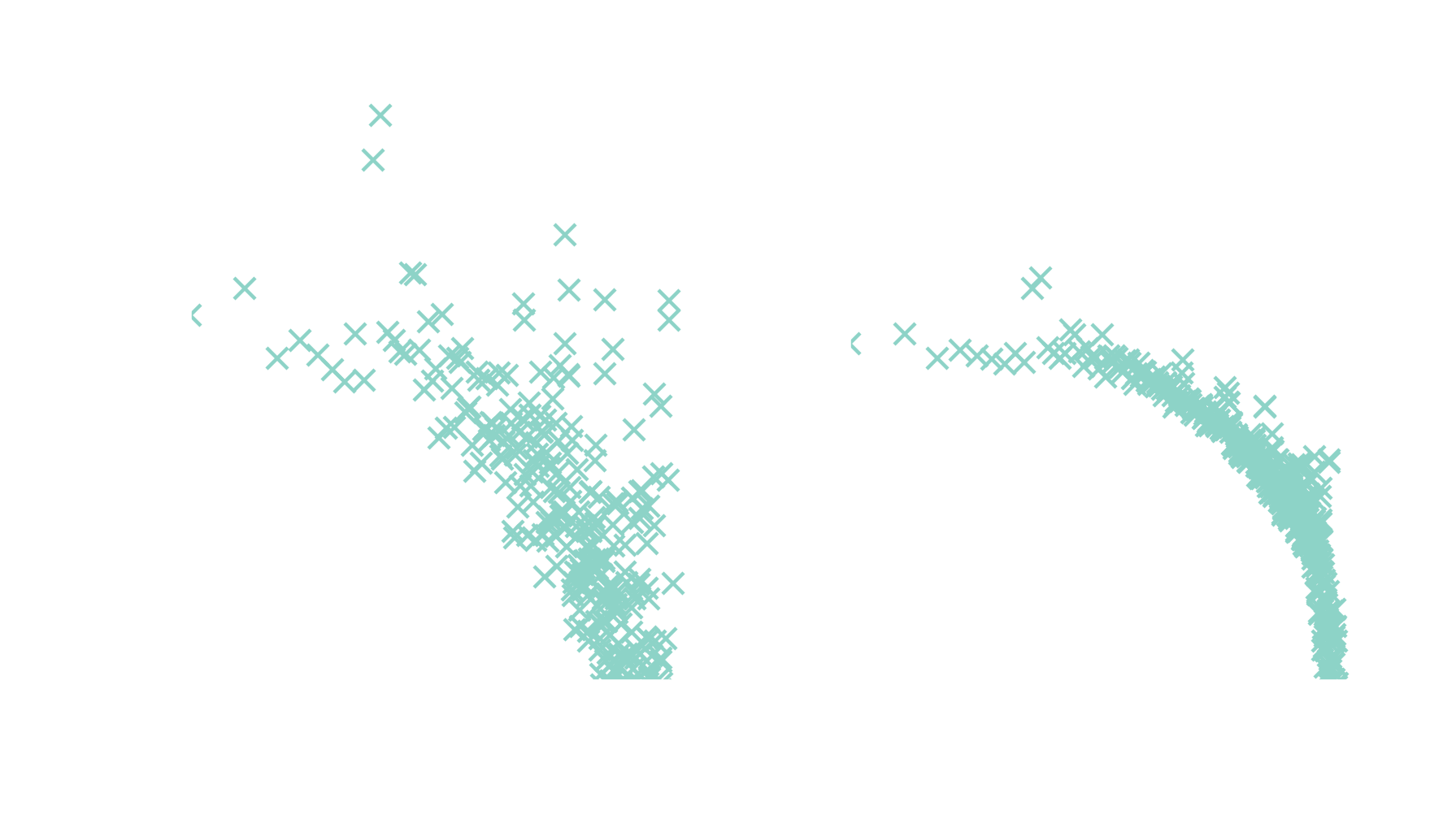
reconstruction error improves from $25\%$ to $5\%$
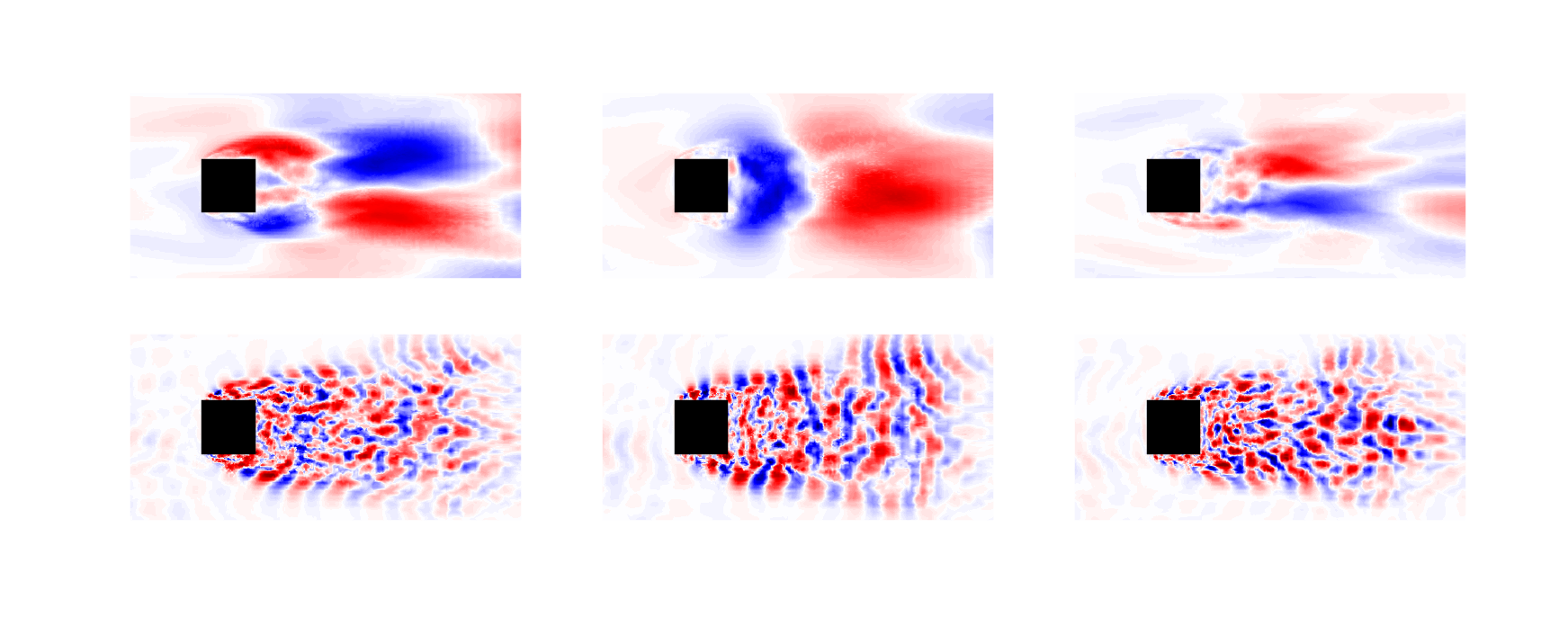
Thank you for you attention!

Slides

GitHub
