Slice of local Mach number $Ma$; $Re_\infty=10^7$, $Ma_\infty=0.75$, $\alpha=4^\circ$.

FOR 2895

Unsteady flow and interaction phenomena at high speed stall conditions

Improved understanding and prediction of flight envelop via:

• experiments: iPSP, PIV, Schlieren, ...
• simulations: LES, RANS, hybrid RANS/LES
• analysis and modeling: modal decomposition, ROMs

Modal decomp. = spatial structures + temp. behavior

spatial mode

temporal coefficient

Common issues/questions in DMD analyses:

• How to construct the state vector?
• Which DMD variant to use?
• How much data is needed?
• How to set the rank parameter?
• How sensitive to noise is the analysis?

$\rightarrow$ (partial) answers in this presentation

Simulation approach

Simulation approach in a nutshell:

• OpenFOAM-v2012
• rhoCentralFoam
• IDDES turbulence modeling
• Spalart-Allmaras closure
• 2D and 3D simulations

github.com/FlowModelingControl/naca0012_shock_buffet

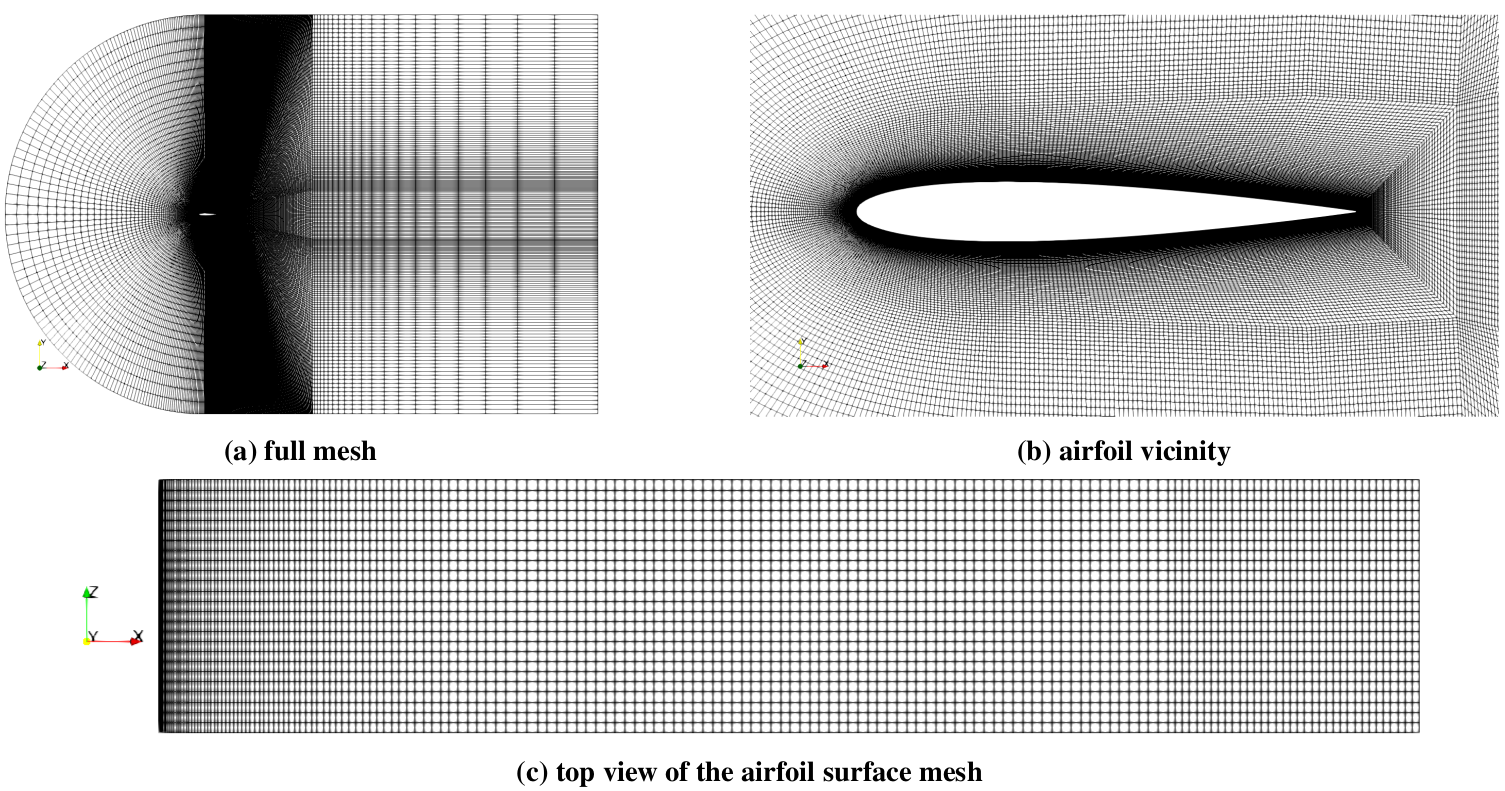
Various views of the computational mesh.

Dynamic mode decomposition

Degrees of freedom in DMD analysis:

1. State vector definition
2. Data pre-processing
3. Operator approximation
4. Mode amplitude computation
5. Mode selection

Review of DMD variants by P. Schmid

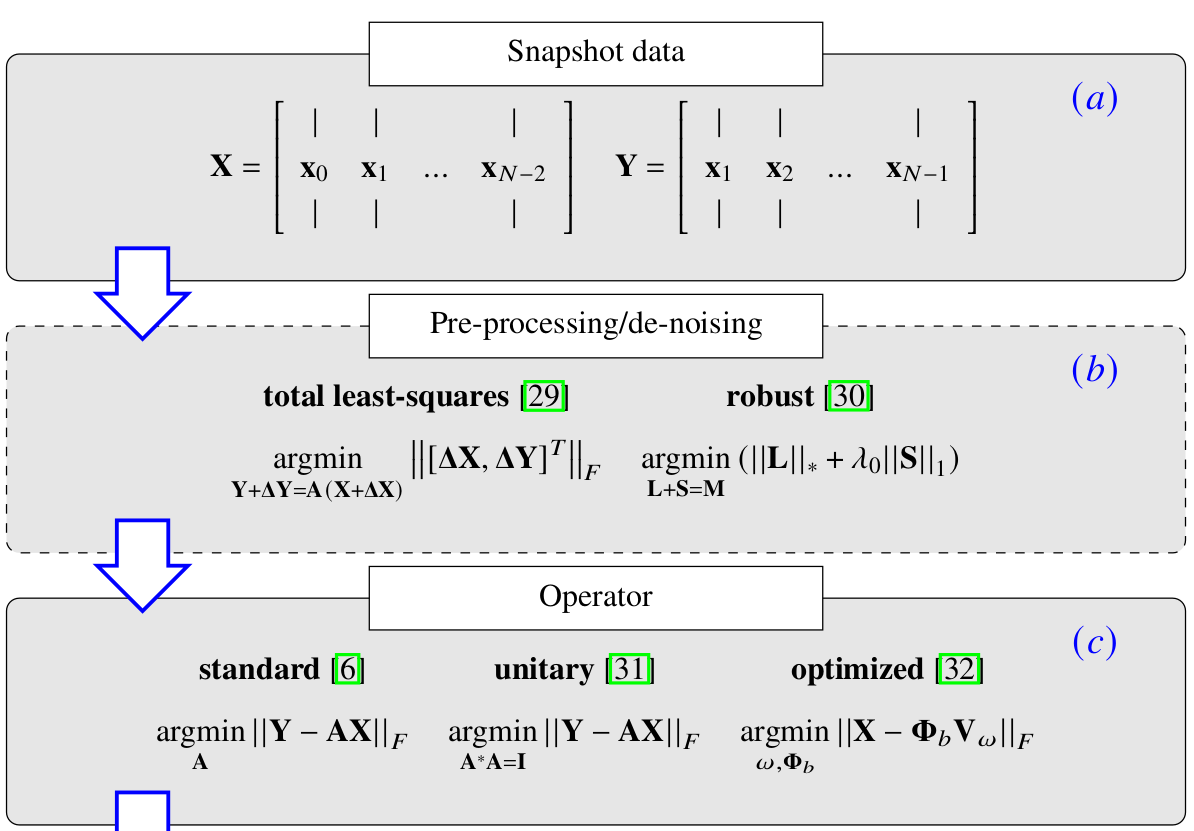
DMD as a five-step analysis - part I.

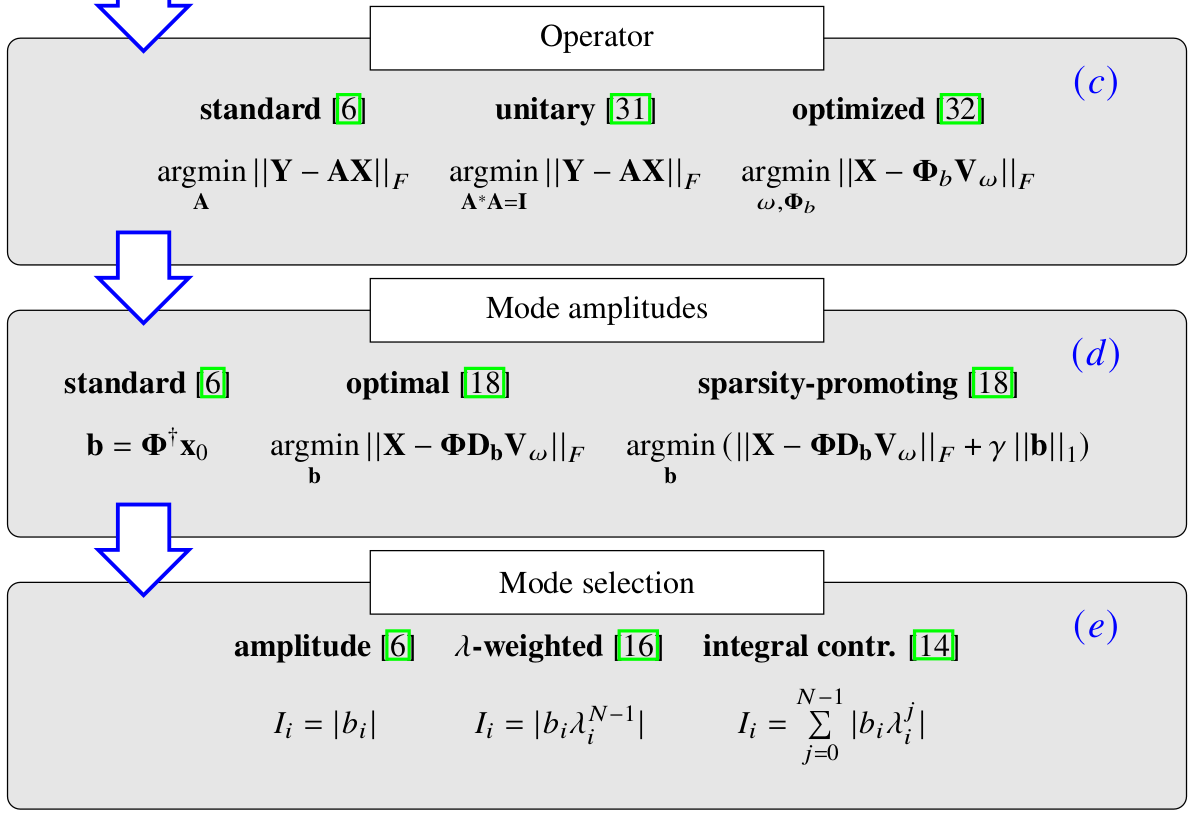
DMD as a five-step analysis - part II.

Abbreviations:

• TDMD - total least squares DMD
• UDMD - unitary DMD operator
• opt. - optimal mode coefficients $\mathbf{b}$
• int. - integral importance measure
• amp. - classical DMD amplitude $|b_i|$

opt. TDMD, int. $\rightarrow$ total least-squares DMD with optimal amplitudes and integral mode selection.

Test of state vectors and DMD variants

Test 0: variance of state vector norms

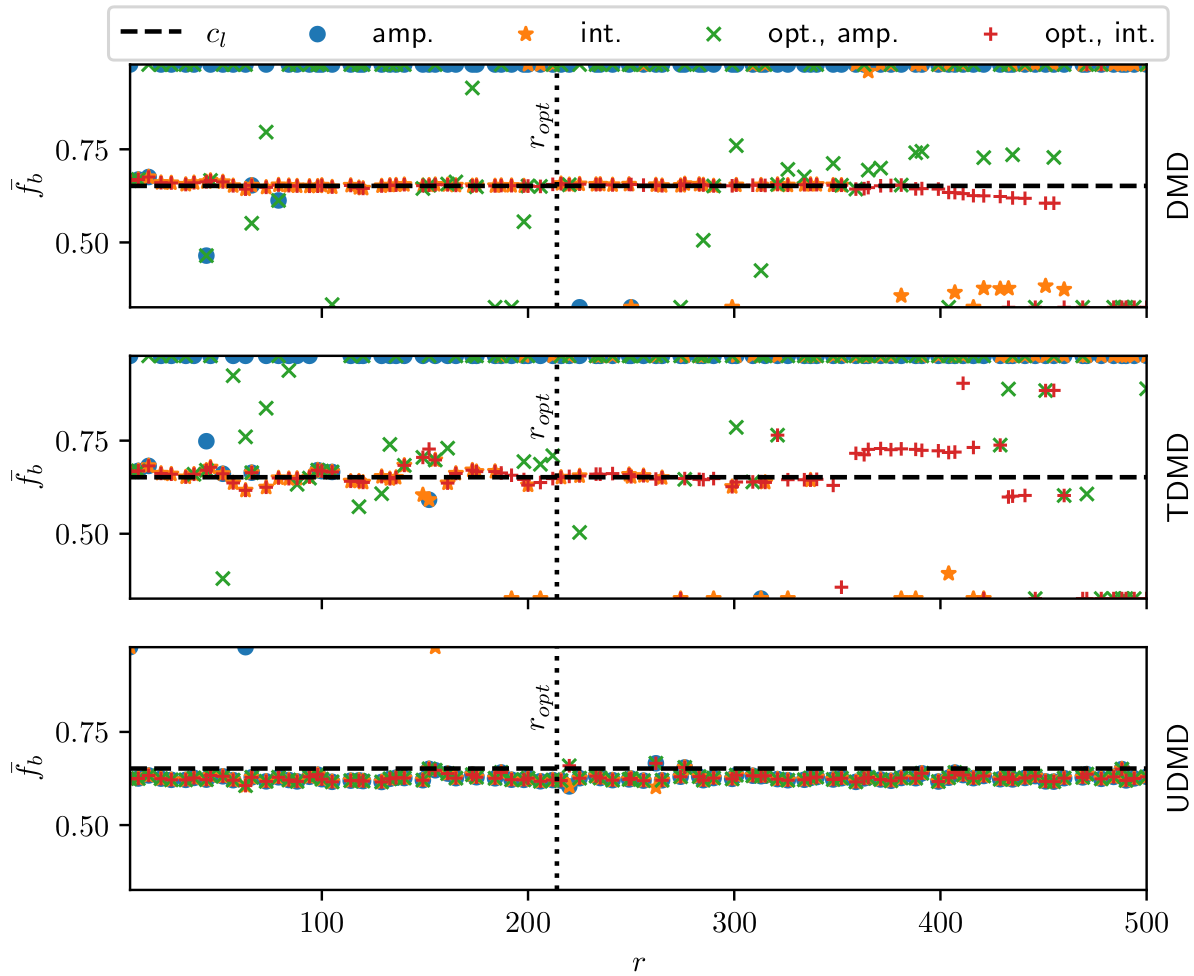
Test 1: rank sensitivity of buffet frequency

Assumption: top mode = buffet mode

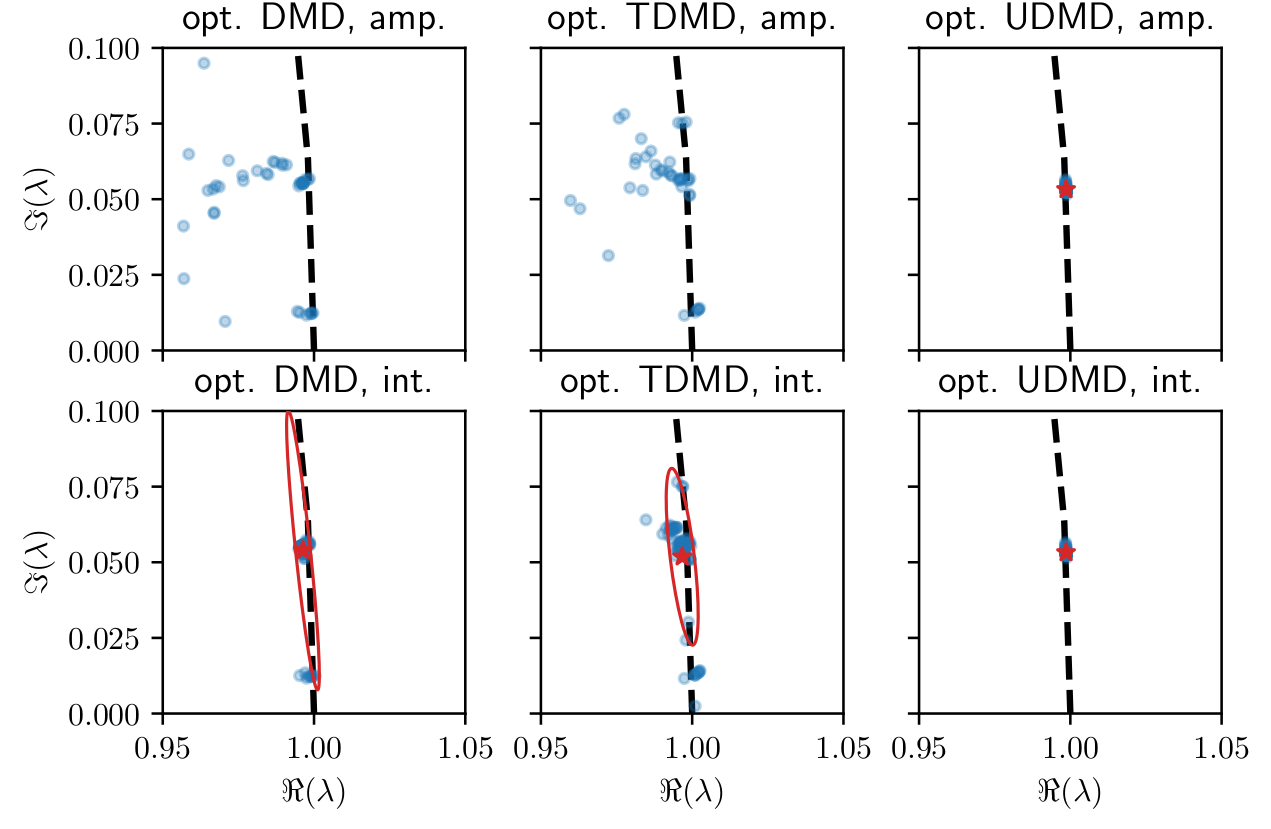
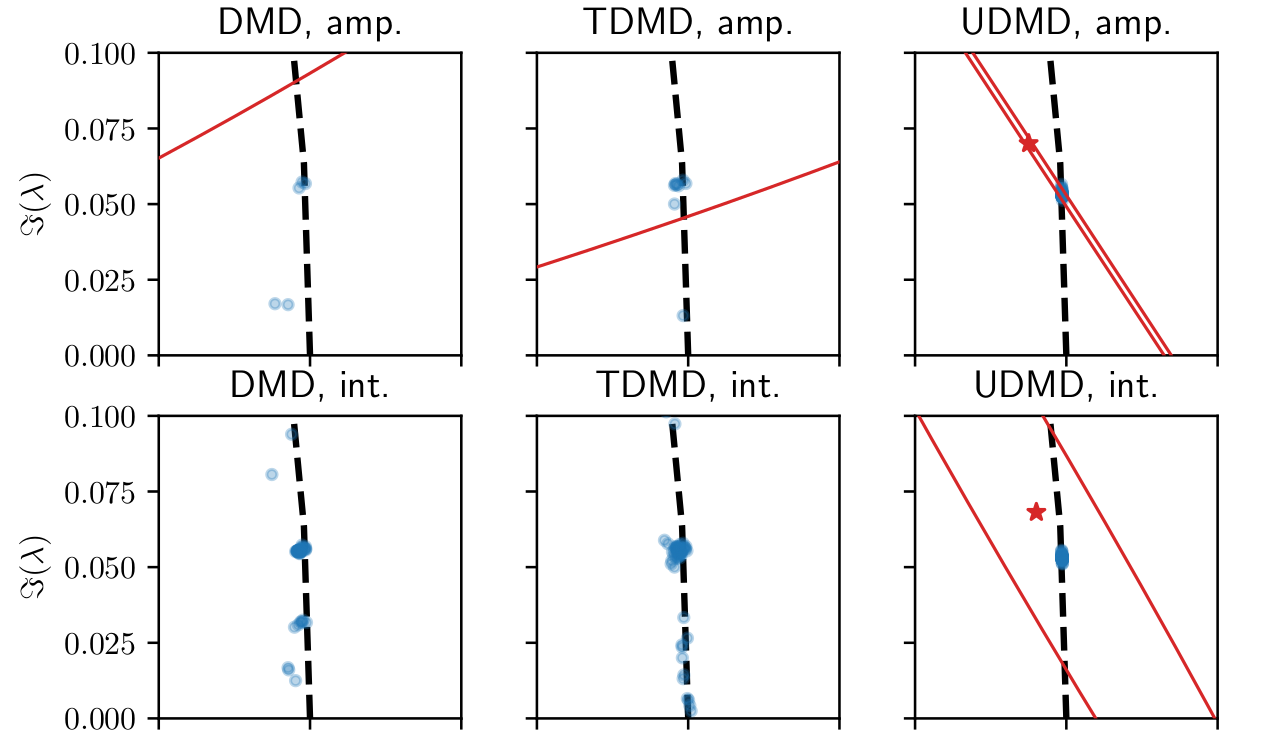
Test 2: sensitivity to the sampling rate

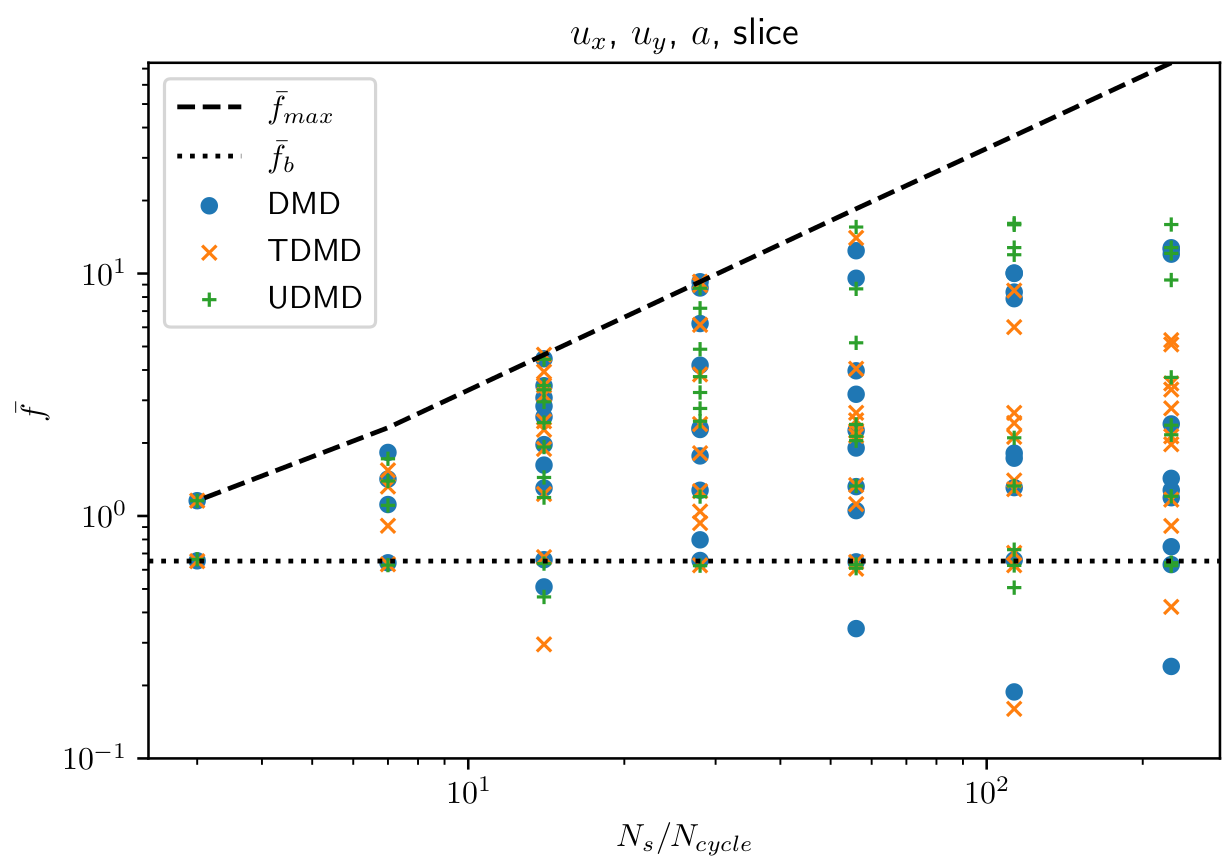
Test 3: rank sensitivity of the full spectrum

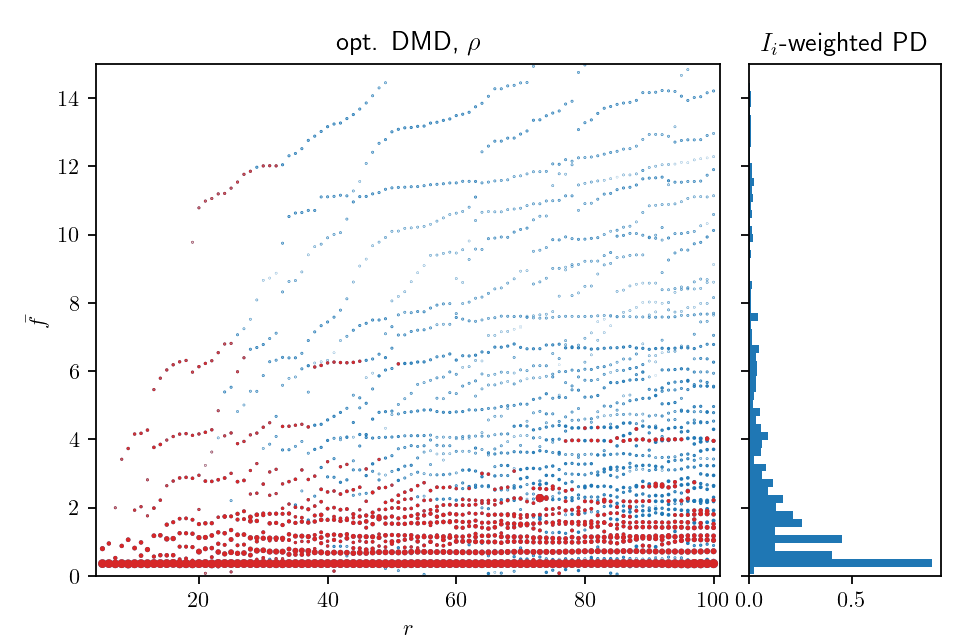
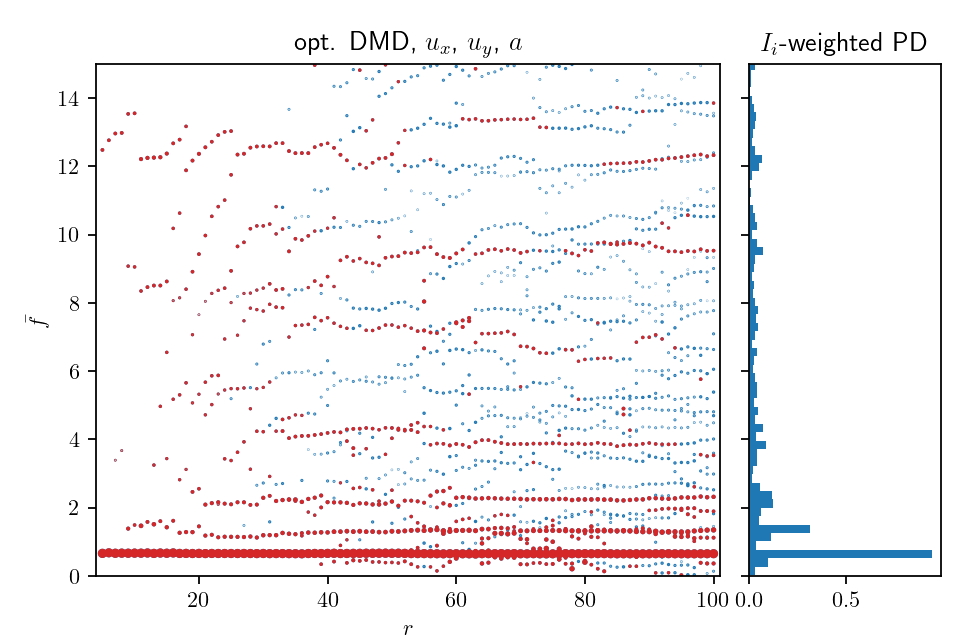
Winning configuration:

• physics-based, weighted state vector
• no additional pre-processing
• standard operator def.
• optimized amplitudes
• integral selection criterion

Selected results

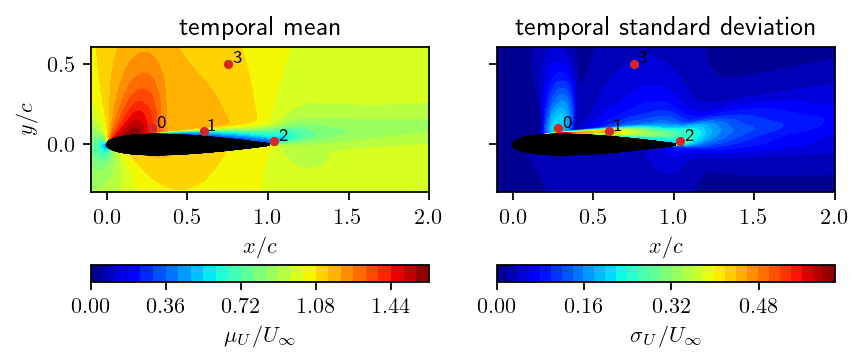
Temporal mean, std., and probe locations.

PSD based on speed at probe locations.

DMD spectrum obtained from slice data.

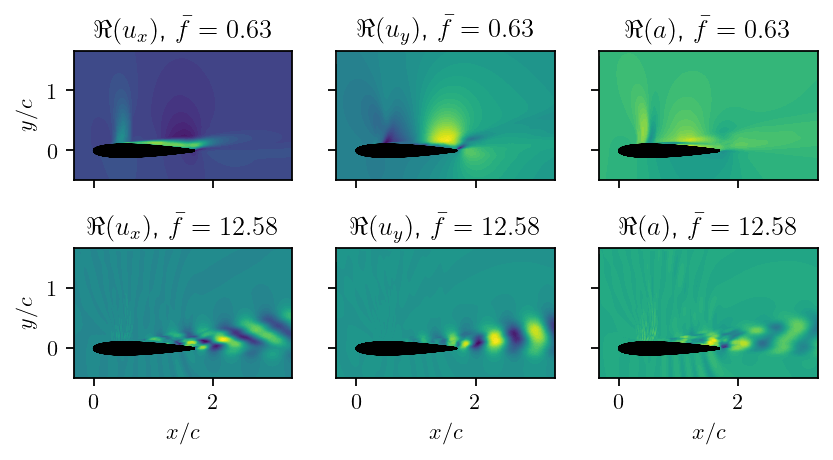
Characteristic DMD modes: shock motion and vortex shedding/acoustic waves.

Mode with vortex shedding and acoustic waves.

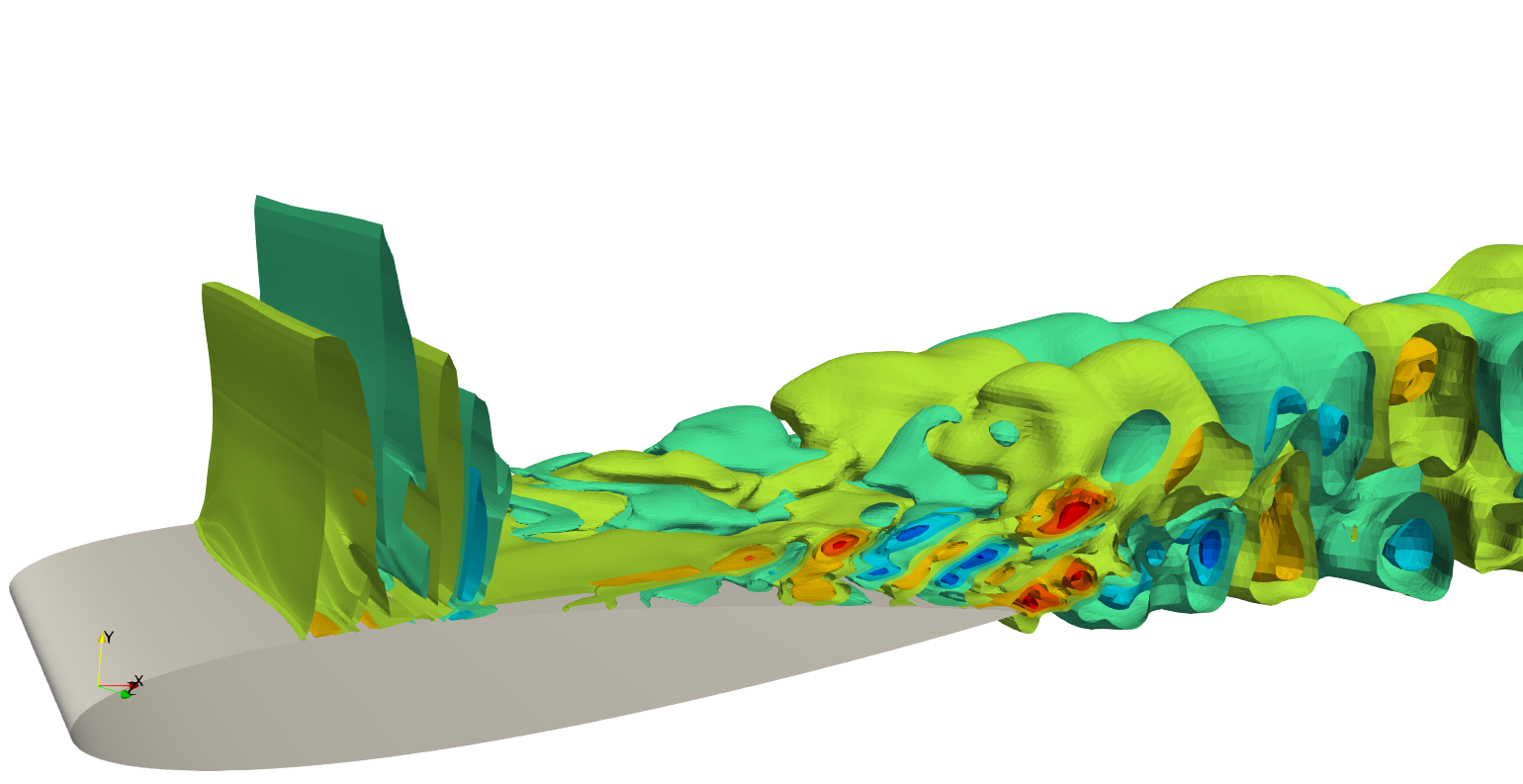
Comparable modes and spectra for volume, slice, and surface data.

Data-driven modeling SIG

• OpenFOAM wiki (overview)
• Github (resource aggregation)
• Upcoming meeting: Sep 2022

THE END

Thank you for you attention!