Active control of the flow past a cylinder using deep reinforcement learning
Andre Weiner, Fabian Gabriel, Darshan Thummar
TU Braunschweig, Institute of Fluid
Mechanics

|
Darshan Thummar: Active flow control in simulations of fluid flows based on DRL, Github |

|
Fabian Gabriel: Active control of the flow past a cylinder under Reynolds number variation using DRL, Github |
Outline
- Flow control problem
- Proximal Policy Optimization (PPO)
- Implementation in OpenFOAM and PyTorch
- Selected results
- Summary and outlook
- OpenFOAM committee on data-driven modeling
Controlling the flow past a cylinder
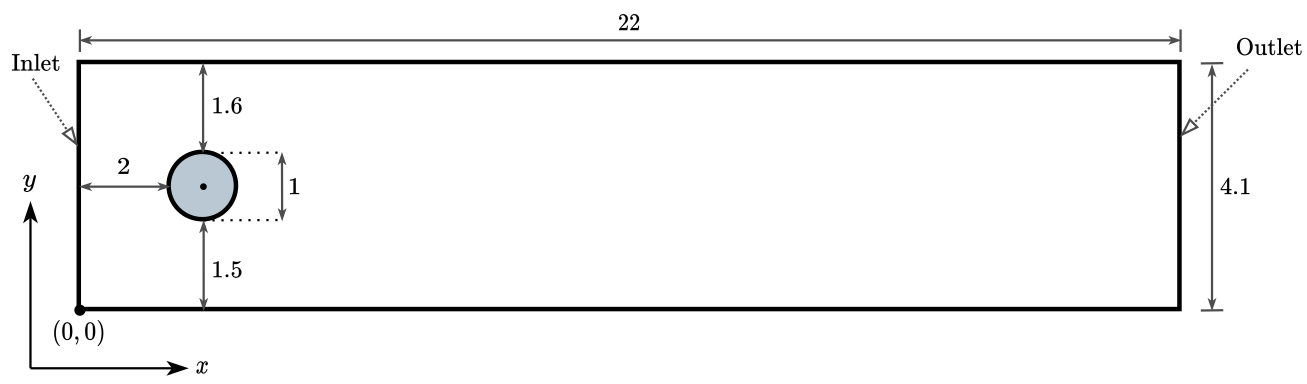
Based on M. Schäfer, S. Turek (1996); $Re=100$; 2D; pimpleFoam.
Flow past a circular cylinder at $Re=100$ - without control.
Can we reduce drag and lift forces?
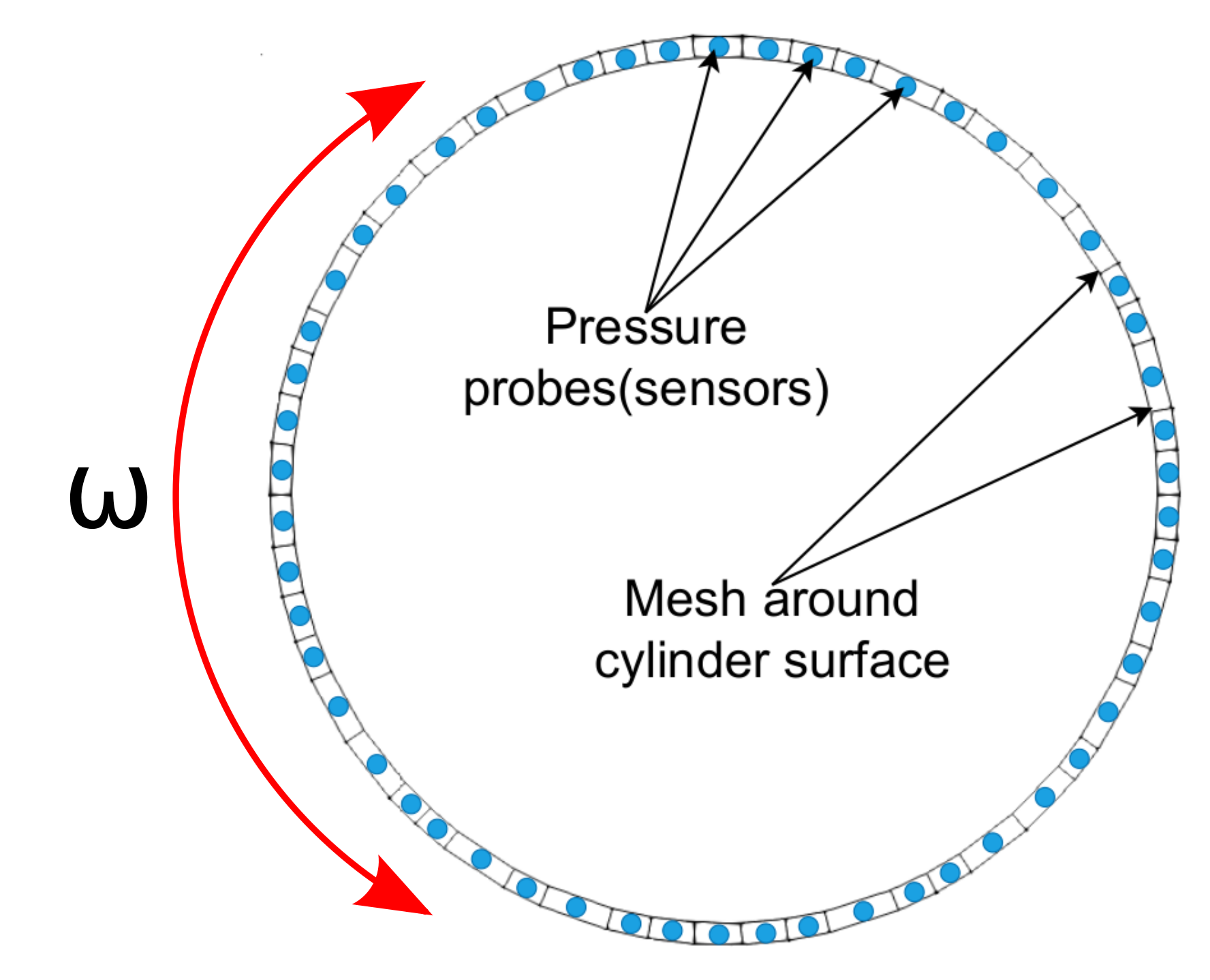
Proximal Policy Optimization (PPO)
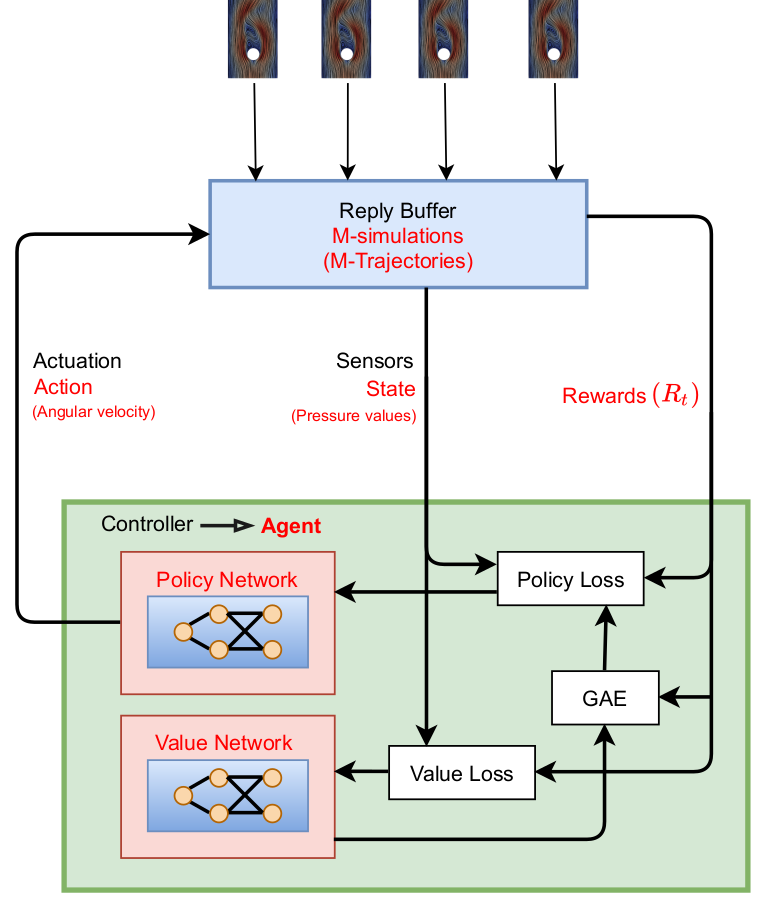
Proximal policy optimization (PPO) workflow (GAE - generalized advantage estimate).
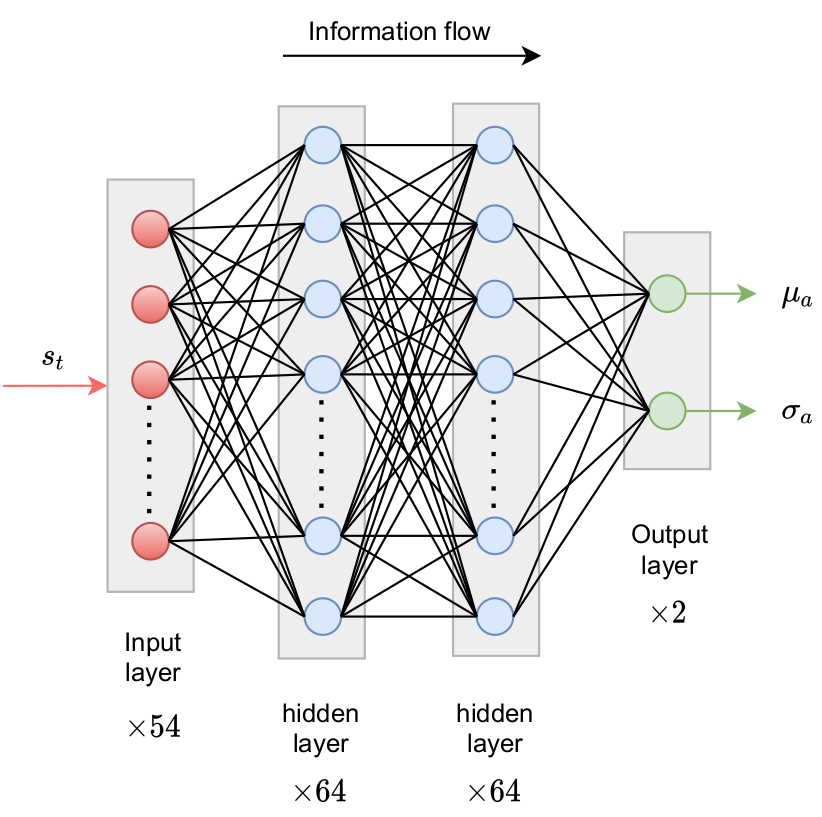
Policy networks outputs parameters of probability density function.
reward at time $t$
$$ R_t = r_0 - \left( r_1 c_D + r_2 |c_L| + r_3 |\dot{\theta}| + r_4 |\ddot{\theta}| \right) $$
- $c_D$ - drag coefficient
- $c_L$ - lift coefficient
- $\dot{\theta}$ - angular velocity
- $\ddot{\theta}$ - angular acceleration
- $r_i$ - constants
long-term consequences
$$ G_t = \sum\limits_{l=0}^{N_t-t} \gamma^l R_{t+l} $$
- $t$ - control time step
- $G_t$ - discounted return
- $\gamma$ - discount factor, typically $\gamma=0.99$
- $N_t$ - number of control steps
learning what to expect in a given state - value function loss
$$ L_V = \frac{1}{N_\tau N_t} \sum\limits_{\tau = 1}^{N_\tau}\sum\limits_{t = 1}^{N_t} \left( V(s_t^\tau) - G_t^\tau \right)^2 $$
- $\tau$ - trajectory (single simulation)
- $s_t$ - state/observation (pressure)
- $V$ - parametrized value function
- clipping not included
Was the selected action a good one?
$$\delta_t = R_t + \gamma V(s_{t+1}) - V(s_t) $$ $$ A_t^{GAE} = \sum\limits_{l=0}^{N_t-t} (\gamma \lambda)^l \delta_{t+l} $$
- $\delta_t$ - one-step advantage estimate
- $A_t^{GAE}$ - generalized advantage estimate
- $\lambda$ - smoothing parameter
make good actions more likely - policy objective function
$$ J_\pi = \frac{1}{N_\tau N_t} \sum\limits_{\tau = 1}^{N_\tau}\sum\limits_{t = 1}^{N_t} \left( \frac{\pi(a_t|s_t)}{\pi^{old}(a_t|s_t)} A^{GAE,\tau}_t\right) $$
- $\pi$ - current policy
- $\pi^{old}$ - old policy (previous episode)
- clipping and entropy not included
- $J_\pi$ is maximized
Why PPO?
- continuous and discrete actions spaces
- relatively simple implementation
- restricted (robust) policy updates
- sample efficient
- ...
Refer to R. Paris et al. 2021 and the references therein for similar works employing PPO.
How long does it take?
$$ t_{train} \approx t_{sim,single} \times N_{episodes} $$
current cylinder example:
$$ t_{train} \approx 0.5h \times 50 = 25h $$
How expensive is it?
$$t_{cpu} = t_{train} \times N_{cpu, single} \times N_\tau$$
current cylinder example:
$$ t_{cpu} = 25h \times 4 \times 10 = 1000h $$
Implementation in OpenFOAM and PyTorch
Python/PyTorch
- create policy and value networks
- fill trajectory buffer (run simulations)
- update policy and value networks
- go back to 1. until converged
Implementation follows closely chapter 12 of Miguel Morales's Grokking Deep Reinforcement Learning
C++/OpenFOAM/PyTorch
- read policy network
- sample and apply action
- write trajectory (state-action pairs)
Boundary condition defined in 0/U
cylinder
{
type agentRotatingWallVelocity;
// center of cylinder
origin (0.2 0.2 0.0);
// axis of rotation; normal to 2D domain
axis (0 0 1);
// name of the policy network; must be a torchscript file
policy "policy.pt";
// when to start controlling
startTime 0.01;
// how often to evaluate policy
interval 20;
// if true, the angular velocity is sampled from a Gaussian distribution
// if false, the mean value predicted by the policy is used
train true;
// maximum allowed angular velocity
absOmegaMax 0.05;
}
Selected results
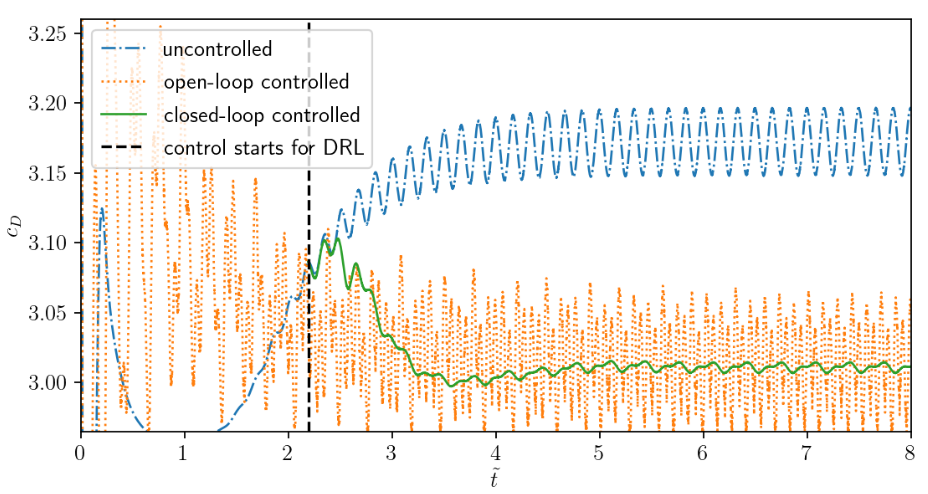
Comparison of uncontrolled, open-loop controlled, and closed-loop controlled drag.
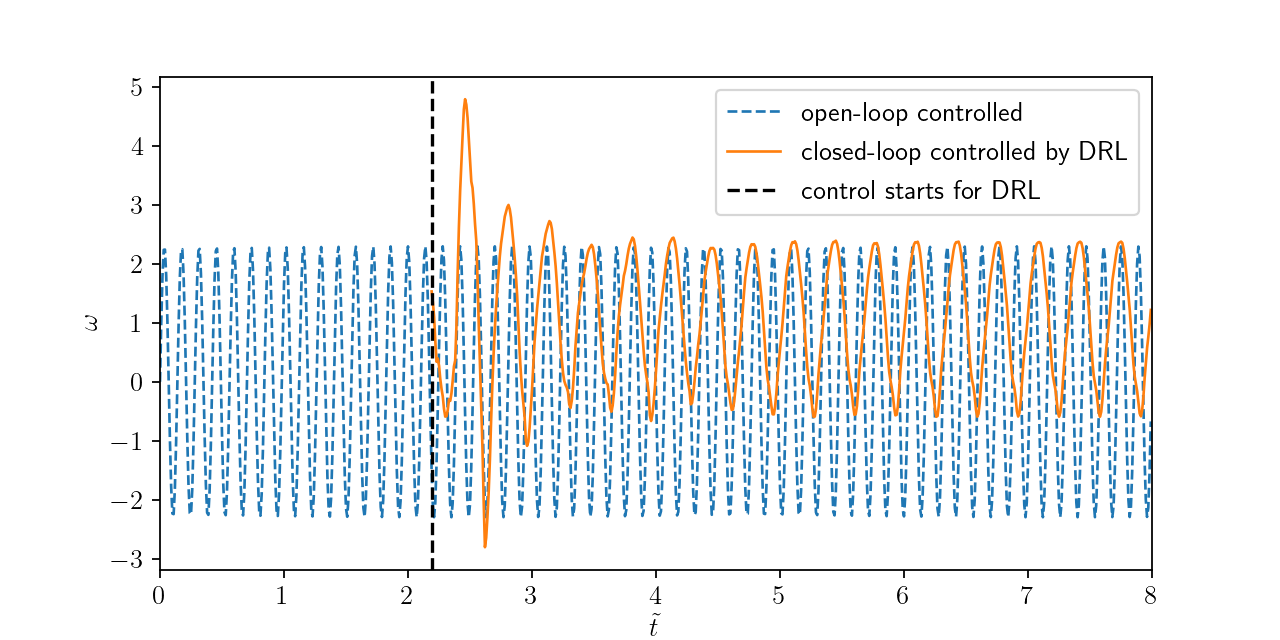
Angular velocity for open and closed-loop control.
How robust is the controller?
- training with steady inlet velocity
$Re=\{100, 200, 400 \}$ - test with unsteady inlet velocity
$Re(t)= 250 + 150\mathrm{sin}(\pi t)$
Variable inlet velocity/Reynolds number $Re(t) = 250 + 150\mathrm{sin}(\pi t)$
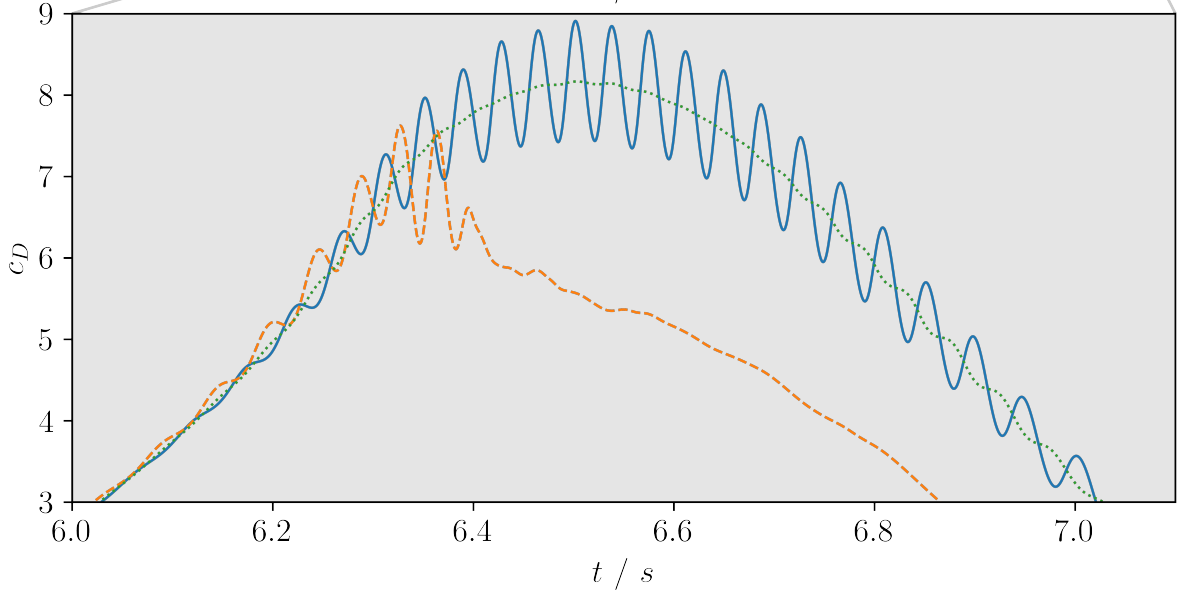
Drag coefficient for transient inlet velocity: uncontrolled and controlled.
Summary
- DRL solves end-to-end control problem
- learned control law appears to be robust
- DRL for real applications is in reach with
OpenFOAM+PyTorch+HPC
Outlook
- extend/modify state (observation)
- model-based PPO extension
- benchmark closed-loop control algorithms
- ad hoc adjustment of control target
- gym-like library based on OpenFOAM
- port DRL to experiment
- ...
Get involved: a.weiner@tu-braunschweig.de
OpenFOAM committee on
data-driven modeling

|

|
| Andre Weiner | Tomislav Marić |
| a.weiner@tu-braunschweig.de | maric@mma.tu-darmstadt.de |
Short and long term objectives available at
https://github.com/AndreWeiner/mlfoam
