What is data?

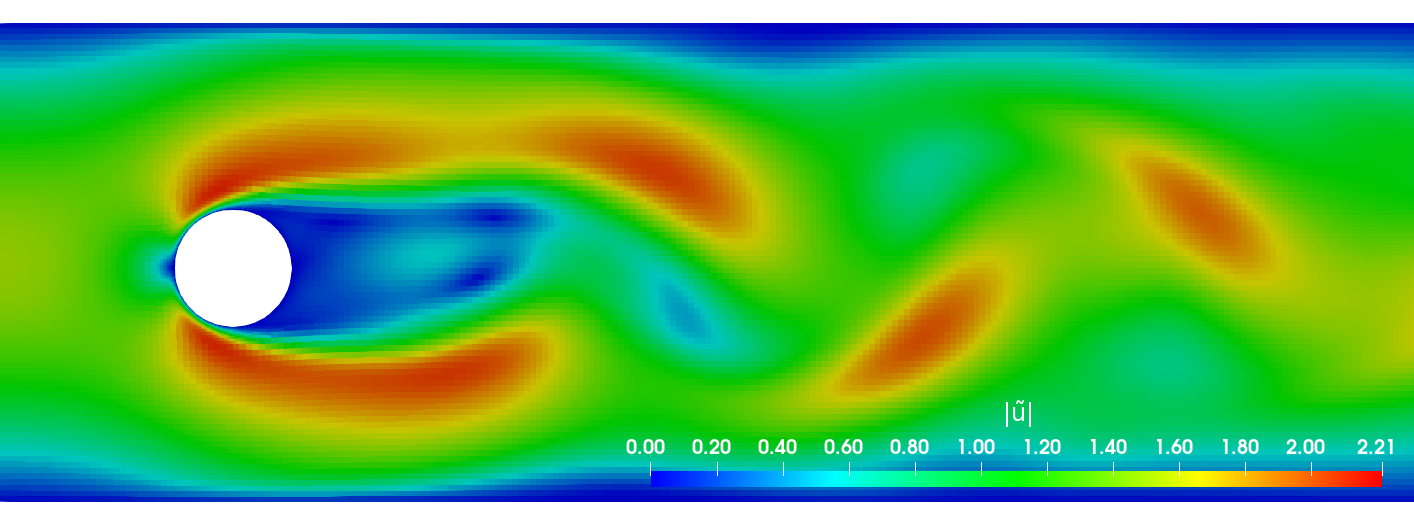
primary data: scalar/vector fields, boundary fields, integral values

# log.rhoPimpleFoam
Courant Number mean: 0.020065182 max: 0.77497916
deltaT = 6.4813615e-07
Time = 1.22219e-06

PIMPLE: iteration 1
diagonal:  Solving for rho, Initial residual = 0, Final residual = 0, No Iterations 0
DILUPBiCGStab:  Solving for Ux, Initial residual = 0.0034181127, Final residual = 6.0056507e-05, No Iterations 1
DILUPBiCGStab:  Solving for Uy, Initial residual = 0.0052004883, Final residual = 0.00012352706, No Iterations 1
DILUPBiCGStab:  Solving for e, Initial residual = 0.06200185, Final residual = 0.0014223046, No Iterations 1
limitTemperature limitT Lower limited 0 (0%) of cells
limitTemperature limitT Upper limited 0 (0%) of cells
limitTemperature limitT Unlimited Tmax 329.54945
Unlimited Tmin 280.90821
					
					
						Checking geometry...
						...
						Mesh has 2 solution (non-empty) directions (1 1 0)
						All edges aligned with or perpendicular to non-empty directions.
						Boundary openness (1.4469362e-19 3.3639901e-21 -2.058499e-13) OK.
						Max cell openness = 2.4668495e-16 OK.
						Max aspect ratio = 3.0216602 OK.
						Minimum face area = 7.0705331e-08. Maximum face area = 0.00033983685.  Face area magnitudes OK.
						Min volume = 1.2975842e-10. Max volume = 6.2366859e-07.  Total volume = 0.0017254212.  Cell volumes OK.
						Mesh non-orthogonality Max: 60.489216 average: 4.0292071
						Non-orthogonality check OK.
						Face pyramids OK.
						Max skewness = 1.1453509 OK.
						Coupled point location match (average 0) OK.
						
				

secondary data: log files, input dictionaries, mesh quality metrics, ...

What is a data-driven workflow?

Example: creating a surrogate or reduced-order model based on numerical data.

Example: creating a space and time dependent boundary condition based on numerical or experimental data.

Example: creating closure models based on numerical data.

Example: active flow control or shape optimization.

ML/deep learning frameworks

• PyTorch
• Tensorflow
• scikit-learn
• Spark MLlib
• ...

criteria: workflow, algorithms, data size, programming language, platform, ...

Getting started

• Github: Docker + OpenFOAM + PyTorch
• accompanying blog post
• article about torch::Sequential by Tomislav Marić
• Github: ML applied to CFD
• Github: boundary layer modeling
• PyTorch C++ examples
• Python and C++ APIs

Supervised learning

Creating a mapping from features to labels based on examples.

Example: mapping the velocity from two-phase to single-phase simulations.

Problem: obtain reference data for local and global mass transfer at high Schmidt ($Sc$) and Péclet ($Pe$) numbers.

bothe@mmm.tu-darmstadt.de

Dimpled-ellipsoidal bubble

Extension to dynamically deforming bubbles together with Irian Hierck, Claire Claassen, and Maike Baltussen @ TU Eindhoven

• Data:
  1. rise velocity
  2. interface position
  3. interface velocity
• PyTorch models:
  1. inlet velocity $\mathbf{u}_{in} = \mathbf{u}_{in}(\tilde{t})$
  2. bubble radius $r_{b} = r_{b}(\tilde{t}, \vartheta)$
  3. surface velocity $\mathbf{u}_{\Sigma} = \mathbf{u}_{\Sigma}(\tilde{t}, \vartheta)$
• OpenFOAM:
  • boundary conditions for velocity and mesh motion

Transient concentration field for different Reynolds numbers $Re$ and constant Schmidt number $Sc=100$.

Mesh motion and zoom view of concentration boundary layer for $Re=569$ and $Sc=100$.

Global Sherwood number $Sh$ for two different mesh resolutions (3250 and 6500 cells/diameter). ~7h, serial, 2.4 GHz

Unsupervised learning

Finding patterns in unlabeled data.

Example: dynamic mode decomposition (DMD) of the flow past a cylinder.

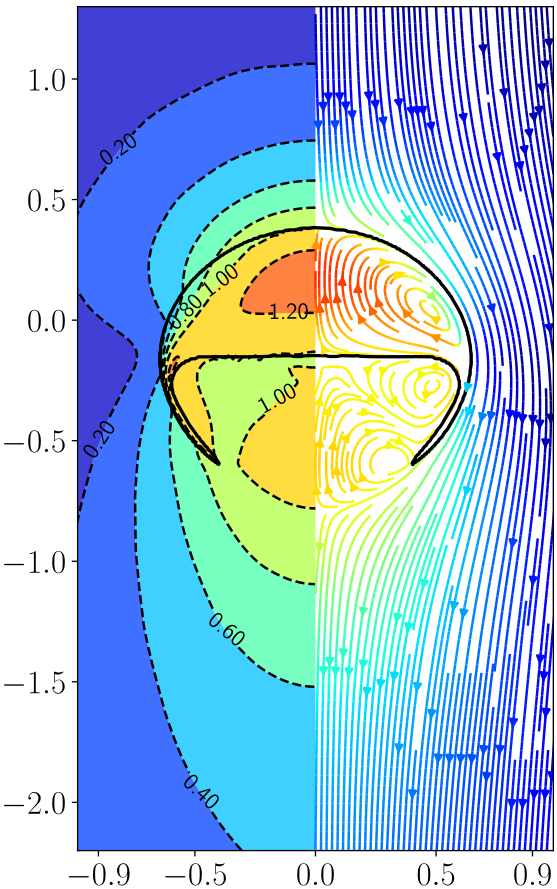
Problem: find a reduced representation based on coherent flow structures. Flow past a cylinder; $Re=100$.

chiara.pesci@esi-group.com

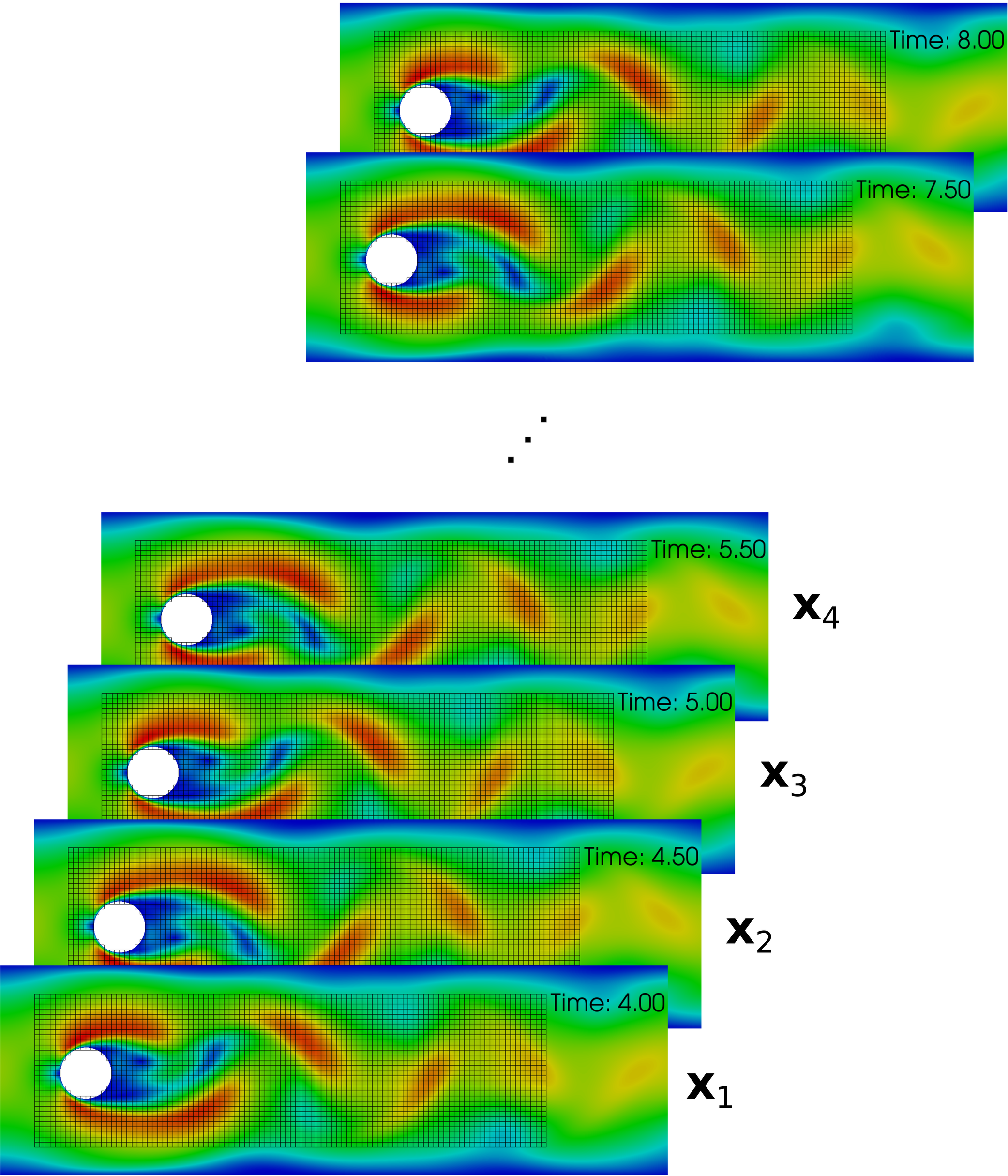
Classical DMD

• data matrices: $$\mathbf{X} = \left[ \mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_{N-1} \right]^T\text{, }\mathbf{X}^\prime = \left[ \mathbf{x}_2, \mathbf{x}_3, \dots, \mathbf{x}_{N} \right]^T$$
• singular value decomposition (SVD): $$\mathbf{X} = \mathbf{U}\mathbf{\Sigma} \mathbf{V}^T$$
• rank $r$ approximation of linear operator: $$ \mathbf{A}=\mathbf{X}^\prime \mathbf{X}^{-1} \text{, } \tilde{\mathbf{A}} = \mathbf{U}^T_r \mathbf{A}\mathbf{U}_r $$
• Eigen-decomposition: $$\tilde{\mathbf{A}}\mathbf{W} = \mathbf{W}\mathbf{\Lambda}\text{, } \Phi = \mathbf{X}^\prime \mathbf{V} \mathbf{\Sigma}^{-1}\mathbf{W}$$

Learn more in this video.

DMD in OpenFOAM

• implemented as function object STDMD (streaming DMD)
• main output:
  • temporal behavior: STDMD.dat in postProcessing
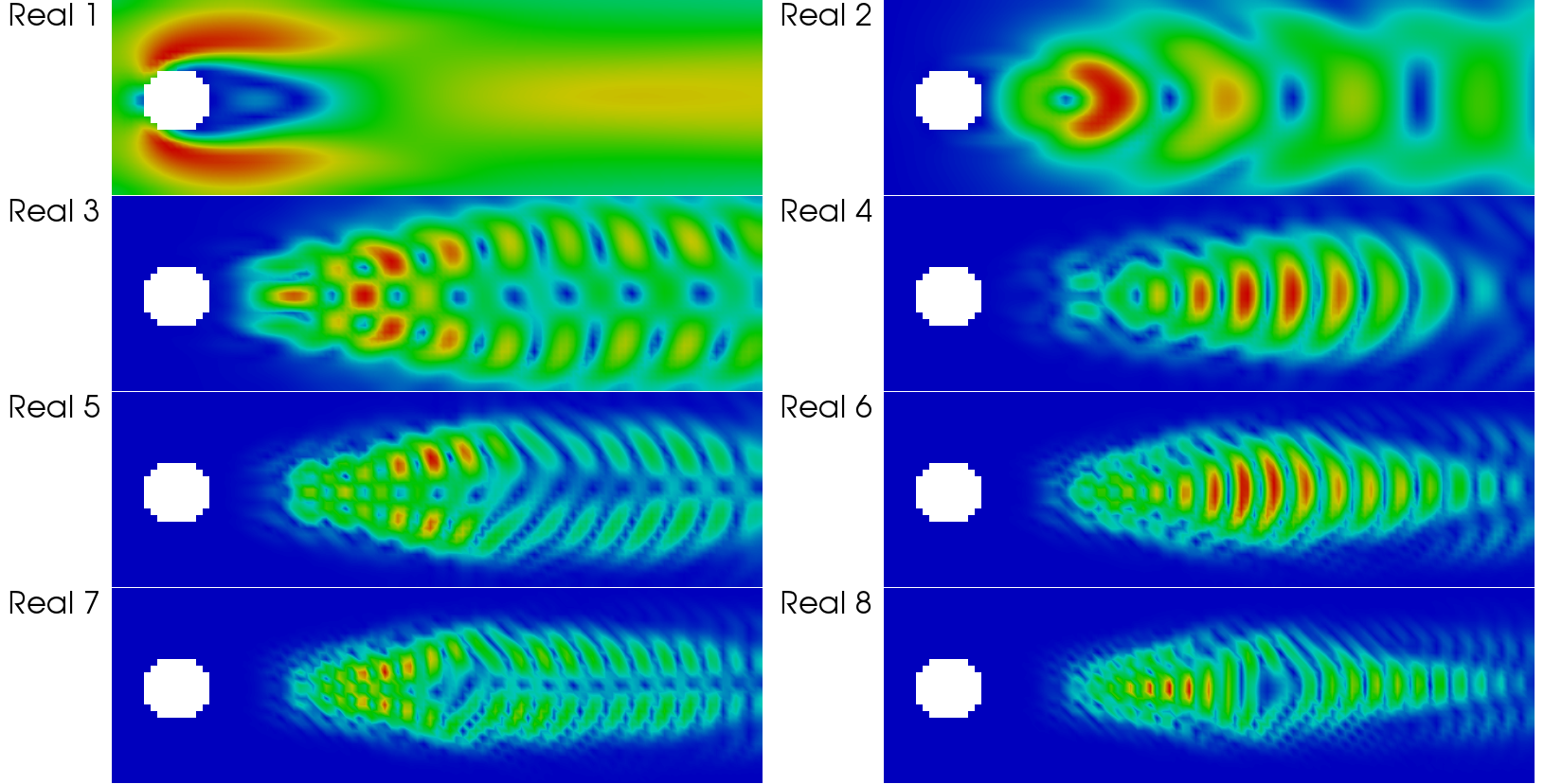
  • spatial modes: modeReal1U in time folders
• What is this useful for?
  • reconstruct fields at any time $t$
  • find and analyze coherent structures
  • build reduced-order models (ROMs)

flowtorch

flowTorch is a unified framework for

1. data loading
2. pre-processing
3. modal decomposition
4. reduced-order models

r.semaan@tu-bs.de

flowTorch in a nutshell

• uses PyTorch as backend (pytorch.org)
• parallel computations on CPUs/GPUs
• mixed precision single/double
• open-source release planned (MIT)
• implemented as a Python library

(Deep) Reinforcement learning

Create an intelligent agent that learns to map states to actions such that cumulative rewards are maximized.

Example: active flow control for drag reduction.

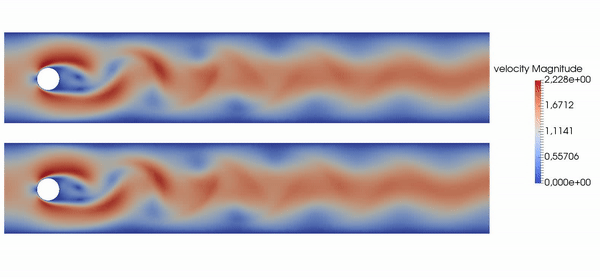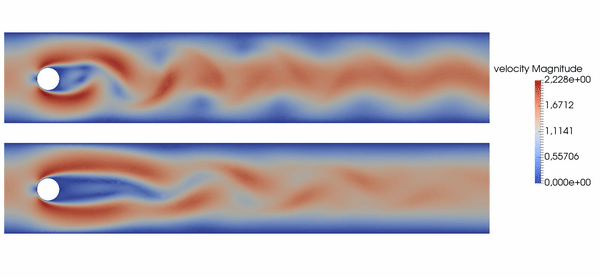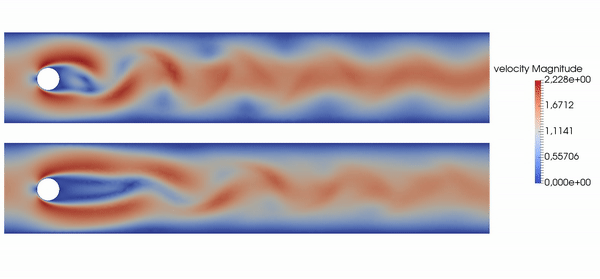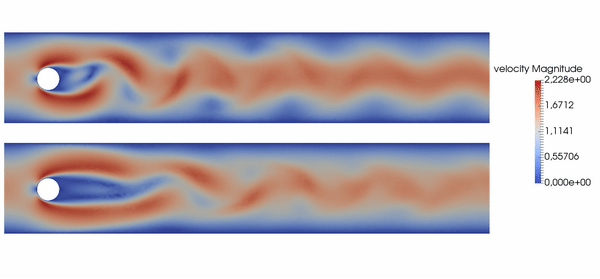
Source: Jean Rabault et al., check out the code! Follow our progress on Github; together with Darshan Thummar.

Example: accelerating OpenFOAM simulations.

Problem: setting inner and outer iterations in $p$-$U$ coupling; linear solver settings.

maric@mma.tu-darmstadt.de

										// system/fvSolution
										p
										{
										  solver      GAMG;
										  smoother    GaussSeidel;
										  tolerance   1e-6;
										  relTol      0.01;
										}
										...
										PIMPLE
										{
										  nOuterCorrectors    50;
										  nCorrectors         1;
										  nNonOrthogonalCorrectors 1;
										  ...
										}