Closed-loop active flow control

Goals of flow control:

• drag reduction
• load reduction
• process intensification
• noise reduction
• ...

Categories of flow control:

1. passive: modification of geometry, topology, fluid, ...
2. active: flow actuation through moving parts, blowing/suction, heating/cooling, ...

Active flow control can be more effective but requires energy.

Categories of active flow control:

1. open-loop: actuation prescript; constant or periodic motion, blowing, heating, ...
2. closed-loop: actuation based on sensor input

Closed-loop flow control can be more effective but defining the control law is extremely challenging.

Closed-loop flow control with variable Reynolds number; source: F. Gabriel 2021.

How to find the control law?

• careful manual design
• adjoint optimization
• machine learning control (MLC)
• (deep) reinforcement learning (DRL)

Favorable attributes of DRL:

• sample efficient thanks to NN-based function approximation
• discrete, continuous, or mixed states and actions
• control law is learnt from scratch
• can deal with uncertainty
• high degree of automation possible

Why CFD-based closed-loop control via DRL?

• save virtual environment
• prior optimization, e.g., sensor placement

Main challenge: CFD environments are expensive!

Reinforcement learning basics

Create an intelligent agent that learns to map states to actions such that cumulative rewards are maximized.

Flow past a cylinder benchmark.

Experience tuple:

$$ \left\{ S_t, A_t, R_{t+1}, S_{t+1}\right\} $$

Trajectory:

$ \left\{S_0, A_0, R_1, S_1\right\} $
$ \left\{S_1, A_1, R_2, S_3\right\} $
$\left\{ ...\right\} $

$r=3-(c_d + 0.1 |c_l|)$

Long-term consequences:

$$ G_t = \sum\limits_{l=0}^{N_t-t} \gamma^l R_{t+l} $$

• $t$ - control time step
• $G_t$ - discounted return
• $\gamma$ - discount factor, typically $\gamma=0.99$
• $N_t$ - number of control steps

DRL learning objective:
maximize expected cumulative rewards.

A close look at proximal policy optimization (PPO)

Why PPO?

• continuous and discrete actions spaces
• relatively simple implementation
• restricted (robust) policy updates
• sample efficient
• ...

Refer to R. Paris et al. 2021 and the references therein for similar works employing PPO.

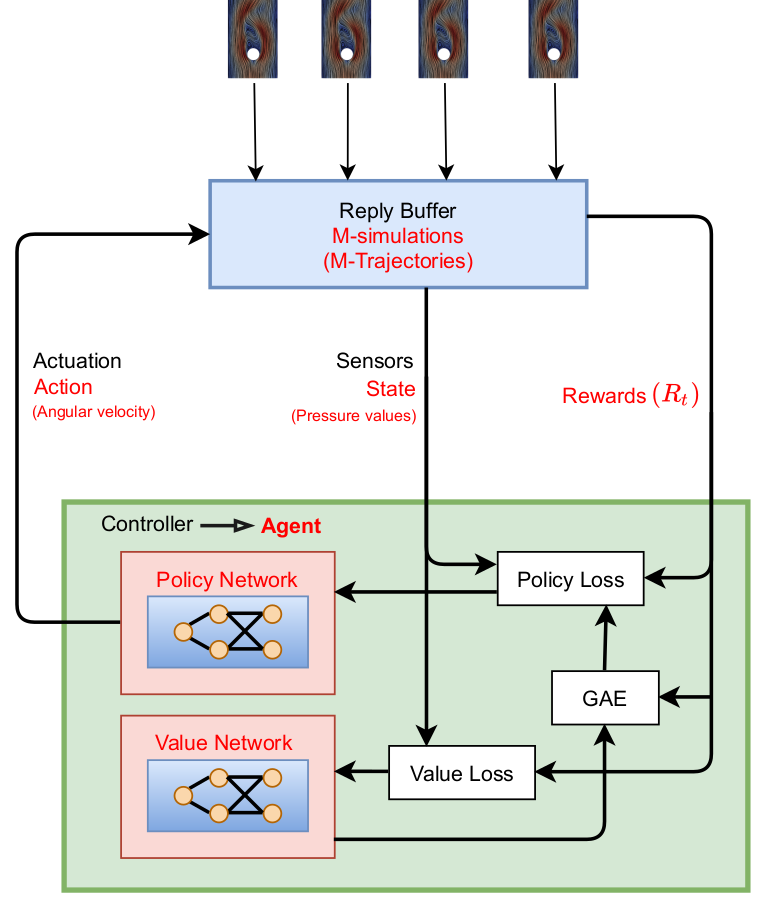
Proximal policy optimization (PPO) workflow (GAE - generalized advantage estimate).

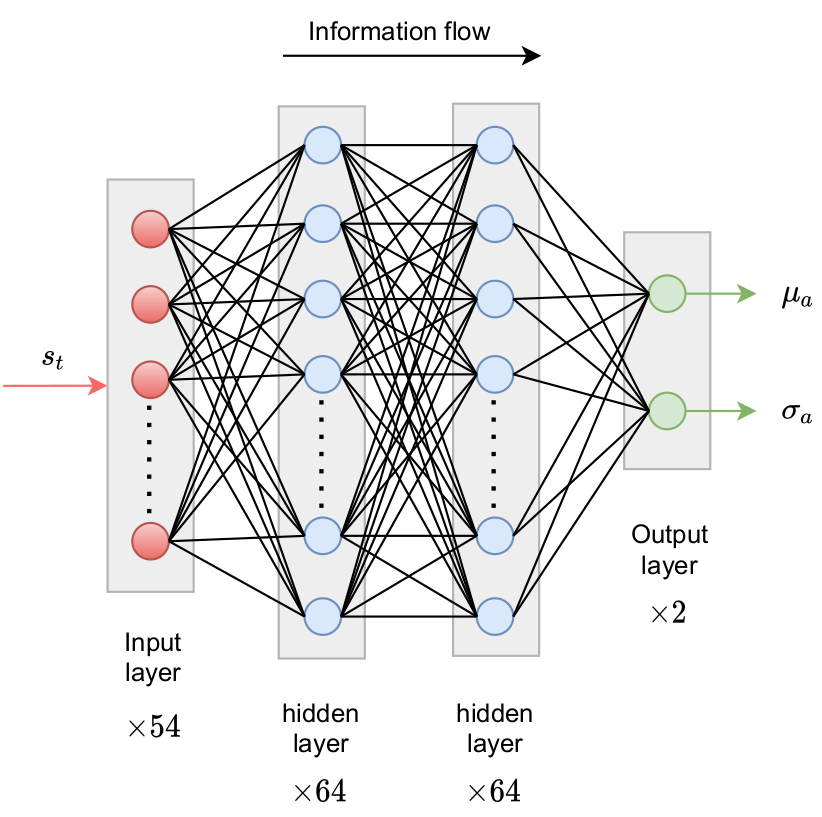
Policy network predicts probability density function(s) for action(s).

Comparison of Gauss and Beta distribution.

learning what to expect in a given state - value function loss

$$ L_V = \frac{1}{N_\tau N_t} \sum\limits_{\tau = 1}^{N_\tau}\sum\limits_{t = 1}^{N_t} \left( V(s_t^\tau) - G_t^\tau \right)^2 $$

• $\tau$ - trajectory (single simulation)
• $s_t$ - state/observation (pressure)
• $V$ - parametrized value function
• clipping not included

Was the selected action a good one?

$$\delta_t = R_t + \gamma V(s_{t+1}) - V(s_t) $$ $$ A_t^{GAE} = \sum\limits_{l=0}^{N_t-t} (\gamma \lambda)^l \delta_{t+l} $$

• $\delta_t$ - one-step advantage estimate
• $A_t^{GAE}$ - generalized advantage estimate
• $\lambda$ - smoothing parameter

make good actions more likely - policy objective function

$$ J_\pi = \frac{1}{N_\tau N_t} \sum\limits_{\tau = 1}^{N_\tau}\sum\limits_{t = 1}^{N_t} \left( \frac{\pi(a_t|s_t)}{\pi^{old}(a_t|s_t)} A^{GAE,\tau}_t\right) $$

• $\pi$ - current policy
• $\pi^{old}$ - old policy (previous episode)
• clipping and entropy not included
• $J_\pi$ is maximized

Optimal sensor placement

Tom Krogmann, Github, 10.5281/zenodo.7636959

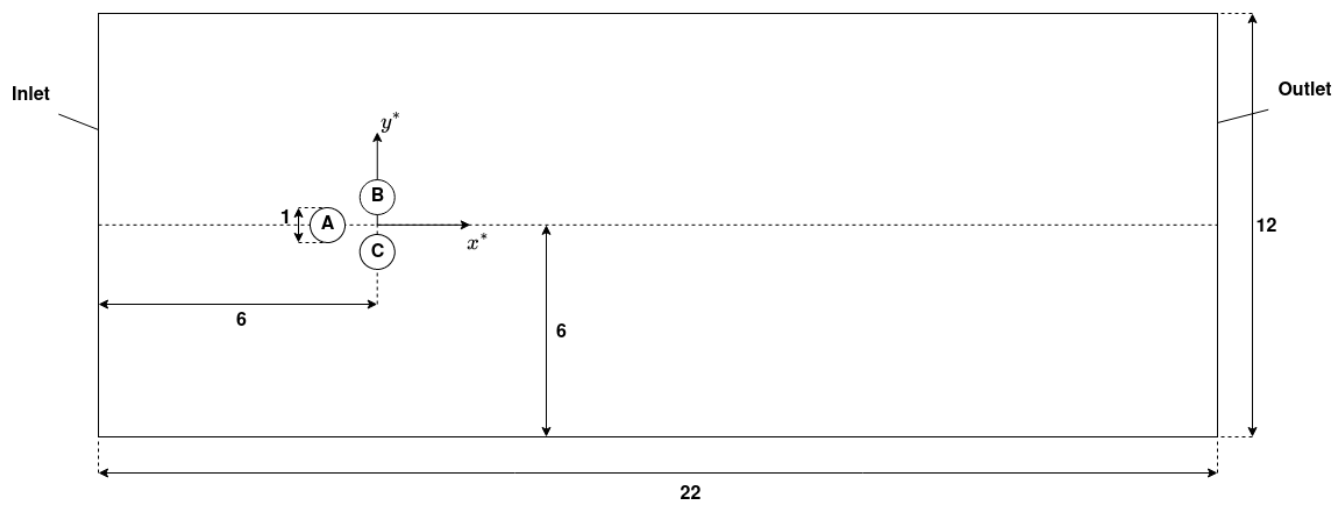
Fluidic pinnball setup.

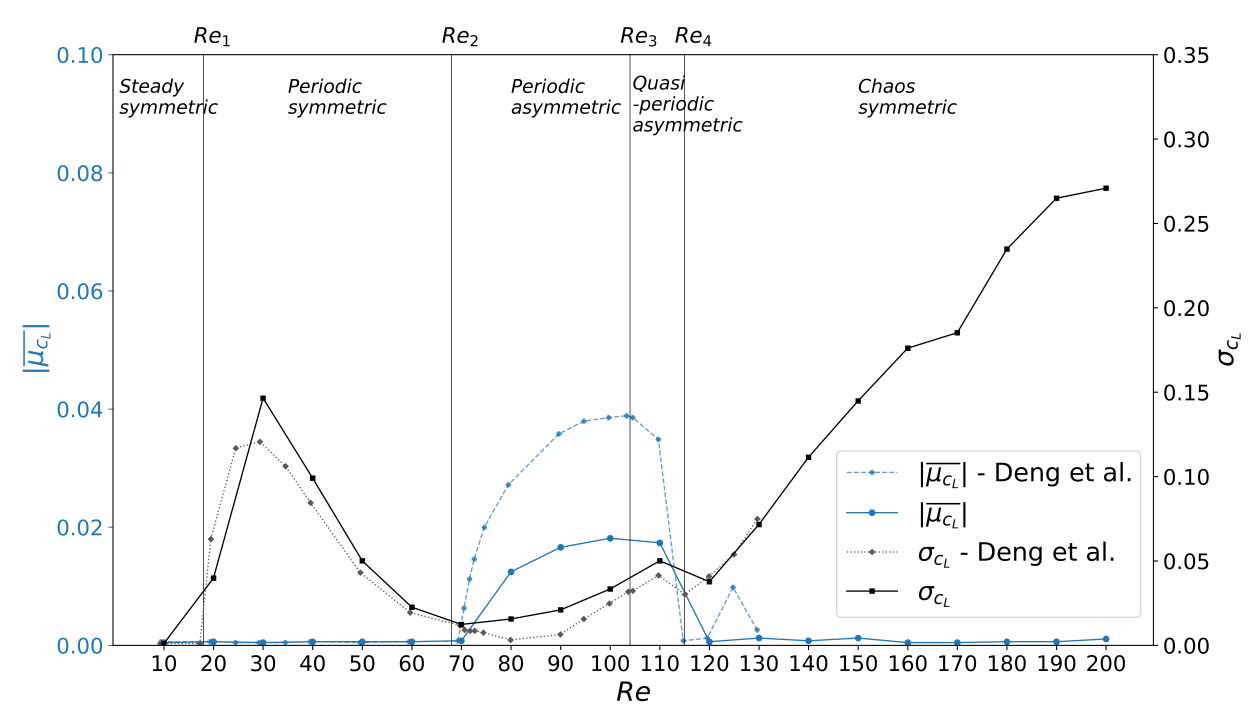
Mean lift $\mu_{c_L}$ over the Reynolds number $Re$.

Challenge with optimal sensor placement and flow control:
actuation changes the dynamical system

Idea: include sensor placement in DRL optimization via attention

Attention: encoder-decoder structure with softmax

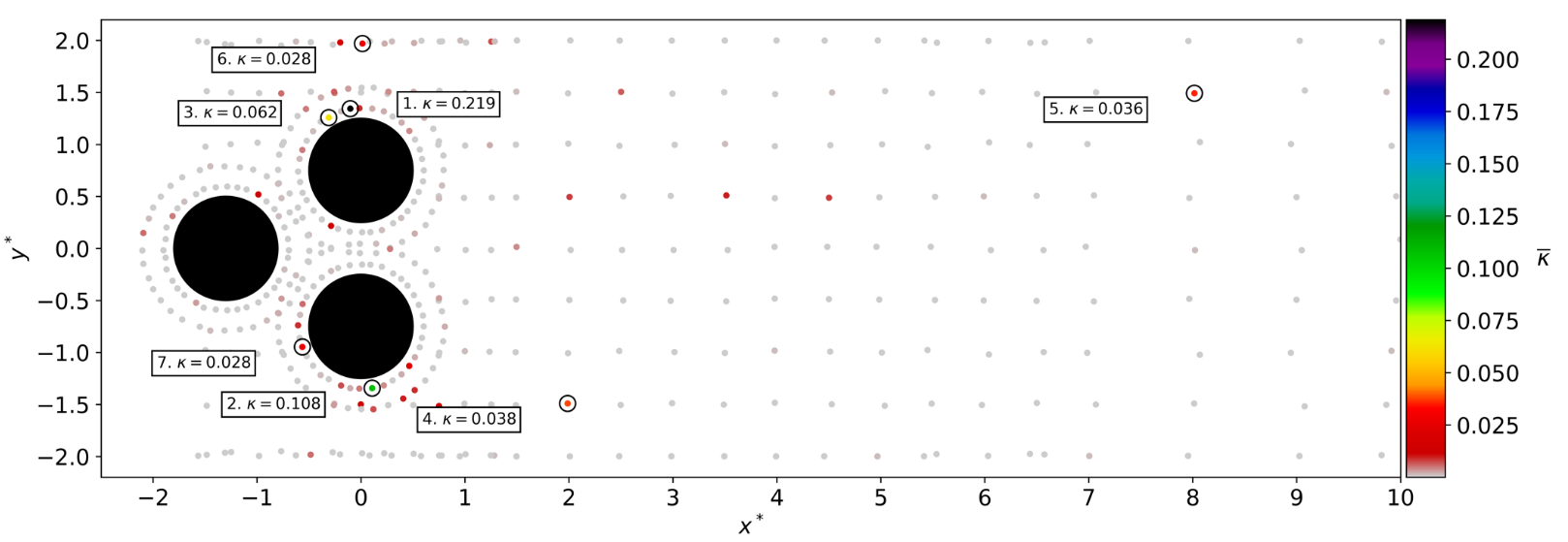
Time-averaged attention weights $\bar{\kappa}$.

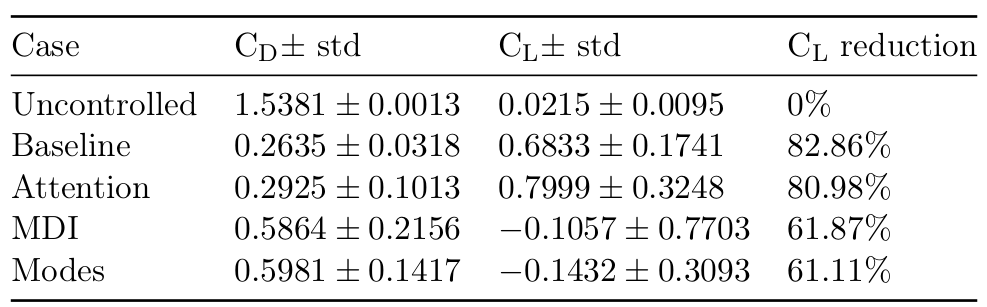
Results obtained with top 7 sensors (MDI - mean decrease of impurity, modes - QR column pivoting).

Accelerated learning with reduced-order models (ROMs)

Janis Geise, Github, 10.5281/zenodo.7642927

Idea: replace CFD with ROM in regular intervals

• model ensemble
• ~30 time delays
• fully-connected, feed-forward

Challenge: automated creation of accurate models.

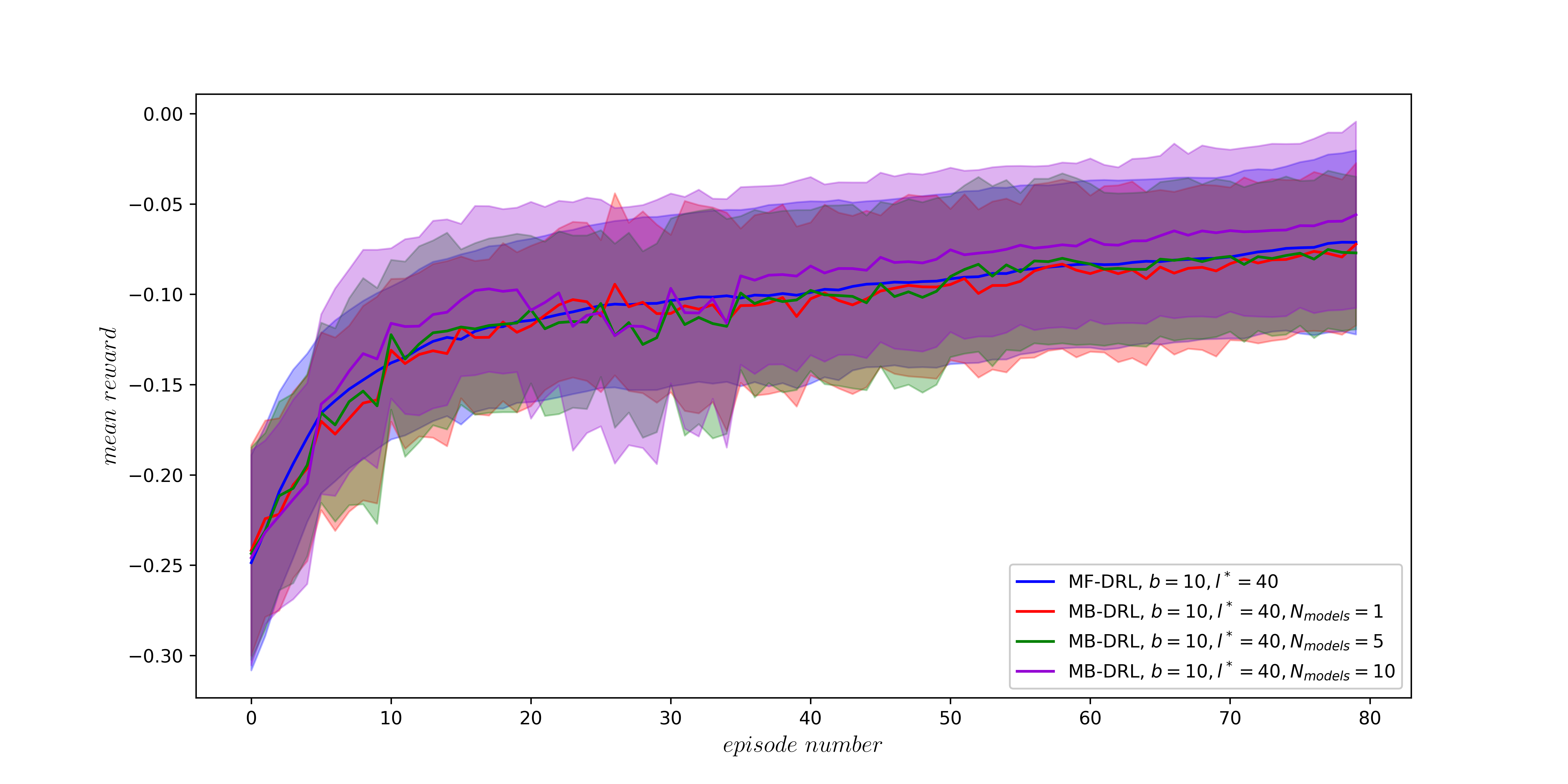
More time savings possible!

THE END

Thank you for you attention!