Slice of local Mach number $Ma$; $Re_\infty=10^7$, $Ma_\infty=0.75$, $\alpha=4^\circ$.

FOR 2895

Unsteady flow and interaction phenomena at high speed stall conditions

Improved understanding and prediction of flight envelop via:

• experiments: iPSP, PIV, Schlieren, ...
• simulations: LES, RANS, hybrid RANS/LES
• analysis and modeling: modal decomposition, ROMs

Modal decomp. = spatial structures + temp. behavior

spatial mode

temporal coefficient

Spectra resulting from standard dynamic mode decomposition (DMD); influence of rank parameter.

Spectra resulting from standard dynamic mode decomposition (DMD); influence of rank parameter.

Problem - determining hyperparameters manually is not always an option:

• large number of datasets
• large datasets
• different data sources
• prior knowledge needed

$\rightarrow$ need for robust automated workflow

SVD and DMD variants

The state vector $\mathbf{x}_n$:

Important: non-uniformly sampled fields should be weighted with square-root of volume/area!

Definition of data matrices:

$$ \mathbf{X} = \left[ \begin{array}{cccc} | & | & & | \\ \mathbf{x}_1 & \mathbf{x}_2 & ... & \mathbf{x}_{N-1} \\ | & | & & | \\ \end{array}\right],\quad \mathbf{X}^\prime = \left[ \begin{array}{cccc} | & | & & | \\ \mathbf{x}_2 & \mathbf{x}_3 & ... & \mathbf{x}_{N} \\ | & | & & | \\ \end{array}\right] $$

$\mathbf{x}_n$ - state vector snapshot at timestep $n$

Singular value decomposition (SVD):

$$ \underset{\tilde{\mathbf{X}}, rank(\tilde{\mathbf{X}})=r}{\mathrm{argmin}} ||\mathbf{X}-\tilde{\mathbf{X}}||_2 = \mathbf{U}_r\mathbf{\Sigma}_r\mathbf{V}_r^\ast $$

• $\mathbf{U}$ - left-singular vectors (spatial structures)
• $\mathbf{\Sigma}$ - singular values (explained variance)
• $\mathbf{V}$ - right-singular vectors (temporal behavior)

Dynamic mode decomposition (DMD):

$$ \underset{\mathbf{A}}{\mathrm{argmin}} ||\mathbf{X}^\prime-\mathbf{AX}||_2 = \mathbf{X}^\prime\mathbf{V}\mathbf{\Sigma}^{-1}\mathbf{U}^\ast $$

• $\mathbf{A}$ - linear operator
• $\mathbf{A}=\mathbf{\Phi\Lambda\Phi}^{-1}$ - modes and dynamics
• $\mathbf{X} \approx \mathbf{U}_r\mathbf{\Sigma}_r \mathbf{V}_r^\ast$

$\rightarrow r$ is a DMD hyperparameter!

How to choose $r$?

Optimal hard threshold for singular values

Optimizing mode amplitudes:

$$ \underset{\mathbf{b}}{\mathrm{argmin}} ||\mathbf{X}-\mathbf{\Phi D}_\mathbf{b}\mathbf{V}_\lambda||_2 $$

• $\mathbf{D}_\mathbf{b} = \mathrm{diag}(\mathbf{b})$
• $\mathbf{V}_\mathbf{\lambda}$ - Vandermode matrix
• $\mathbf{b} = \mathbf{\Phi}^{-1}\mathbf{x}_0$ - default
• idea: distribute approx. error over time

More details: Sparsity-promoting DMD

How to select important modes?

$$ I_i = |\mathbf{\phi}_i|^2 \sum\limits_{j=1}^N b_i \lambda_i^{j-1} $$

• $I_i$ - importance of mode $\mathbf{\phi}_i$
• combination of spatial and temporal variation

More details: K. Kou and W. Zhang

Other tested DMD variants:

• total least squares DMD
• forward-backward DMD
• sparsity-promoting DMD
• ...

See also: pyDMD

Final recipe:

1. select $r$ using SV-HT
2. optimize mode amplitudes
3. sort by "integral" importance

Implementation details: flowTorch - a Python library for the analysis and modeling of fluid flows

Numerical simulations

Setup motivated by exp. investigations of McDevitt and Okuno 1985:

• NACA-0012 airfoil
• $Re_\infty = 10^7$
• $Ma_\infty = 0.75$
• pre-onset: $\alpha = 2^\circ$
• post-onset: $\alpha = 4^\circ$

https://doi.org/10.2514/6.2022-2591

Simulation approach in a nutshell:

• OpenFOAM-v2012
• rhoCentralFoam
• IDDES turbulence modeling
• Spalart-Allmaras closure
• 2D and 3D simulations

github.com/AndreWeiner/naca0012_shock_buffet

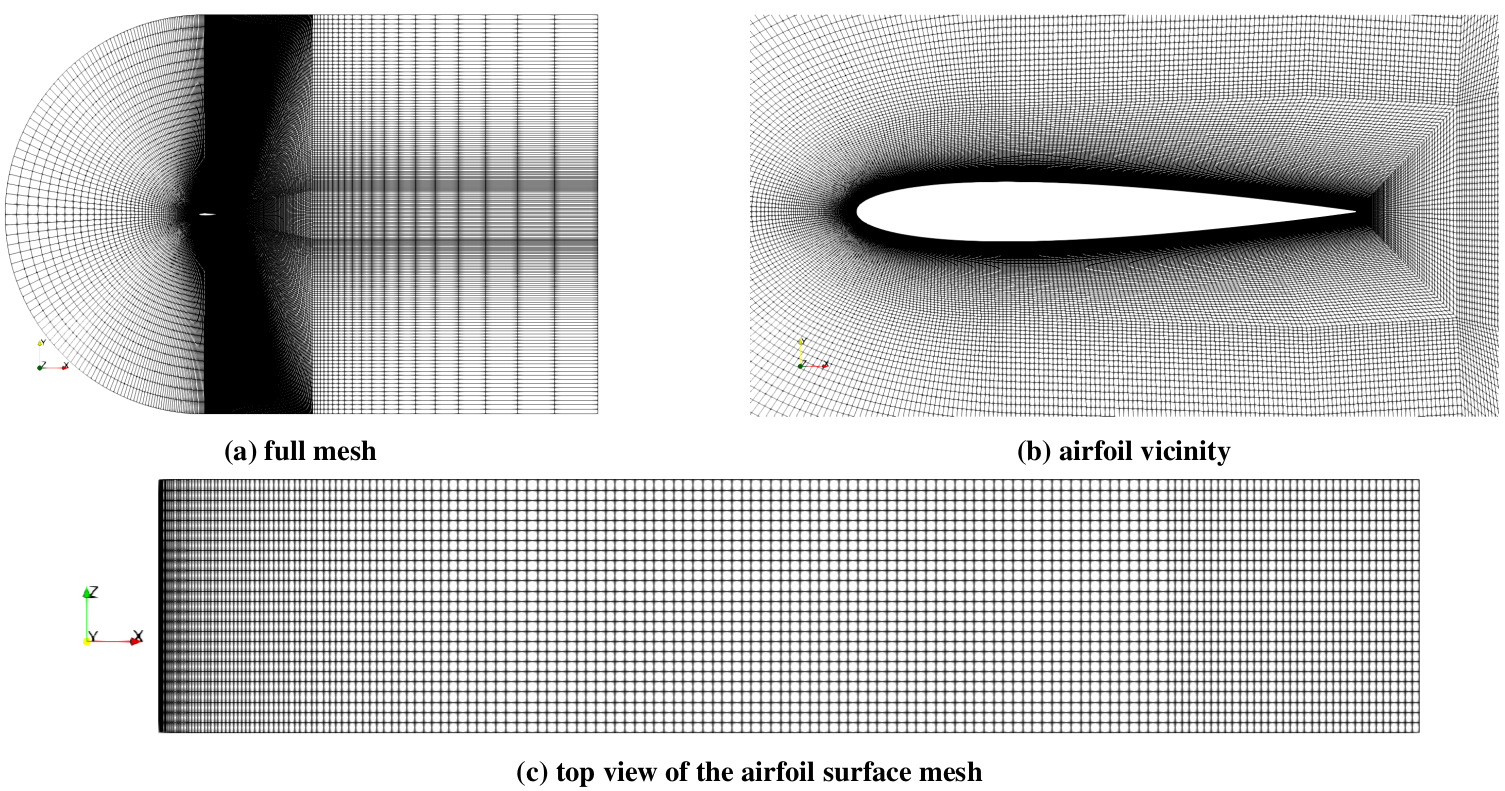
Various views of the computational mesh.

Pressure coefficient $c_p$ at pre-onset conditions, 2D, $\alpha = 2^\circ$.

Pressure coefficient $c_p$ at post-onset conditions, 2D, $\alpha = 4^\circ$.

Results

Influence of volume-weighting on left-singular vectors.

Influence of snapshots/cycle on dominant $\bar{f}$.

DMD buffet mode recon. based on surface $c_p$.

DMD buffet mode recon. based on slice of $u_x$.

Reconstruction of another dominant DMD mode; based on slice of $u_x$.

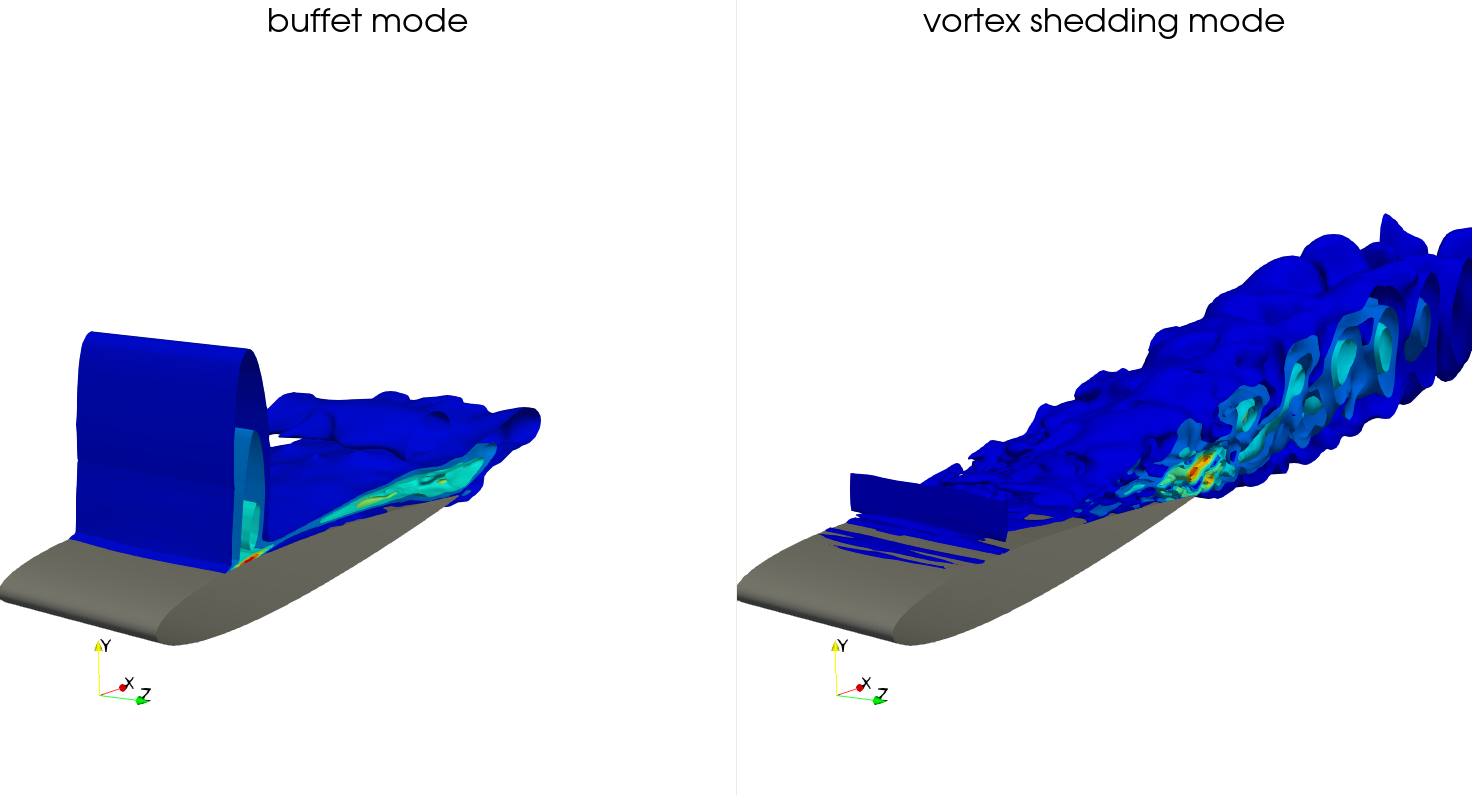
Iso-contours of reconstructed $|\mathbf{u}|$ for two dominant DMD modes.

Summary and outlook

Summary

• robust workflow based on SVD and/or DMD
• volume-weighting of state vector
• comparable spectra for different data sources
• tools, workflow, and data publicly available
• (works also for exp. data)

github.com/AndreWeiner/naca0012_shock_buffet

Outlook

• dealing with large data (S-cube)
• additional data sources
• parametrized ROMs for buffeting flows
• models for buffet intensity

THE END

Thank you for you attention!

{a.weiner|r.semaan}@tu-braunschweig.de