A brief literature survey

Contradictions in literature about:

• onset angle of attack
• shock position
• buffet frequency
• dependency on $Ma_\infty$ and $\alpha$
• ...

Main issues:

• high sensitivity to model constants
• incomplete/missing description
• no access to implementation details

Goal: workflow that is fully

• open-source
• reproducible
• transparent

github.com/AndreWeiner/naca0012_shock_buffet

Simulation approach

Simulation approach in a nutshell:

• OpenFOAM-v2012
• rhoCentralFoam
• IDDES turbulence modeling
• Spalart-Allmaras closure
• 2D and 3D simulations

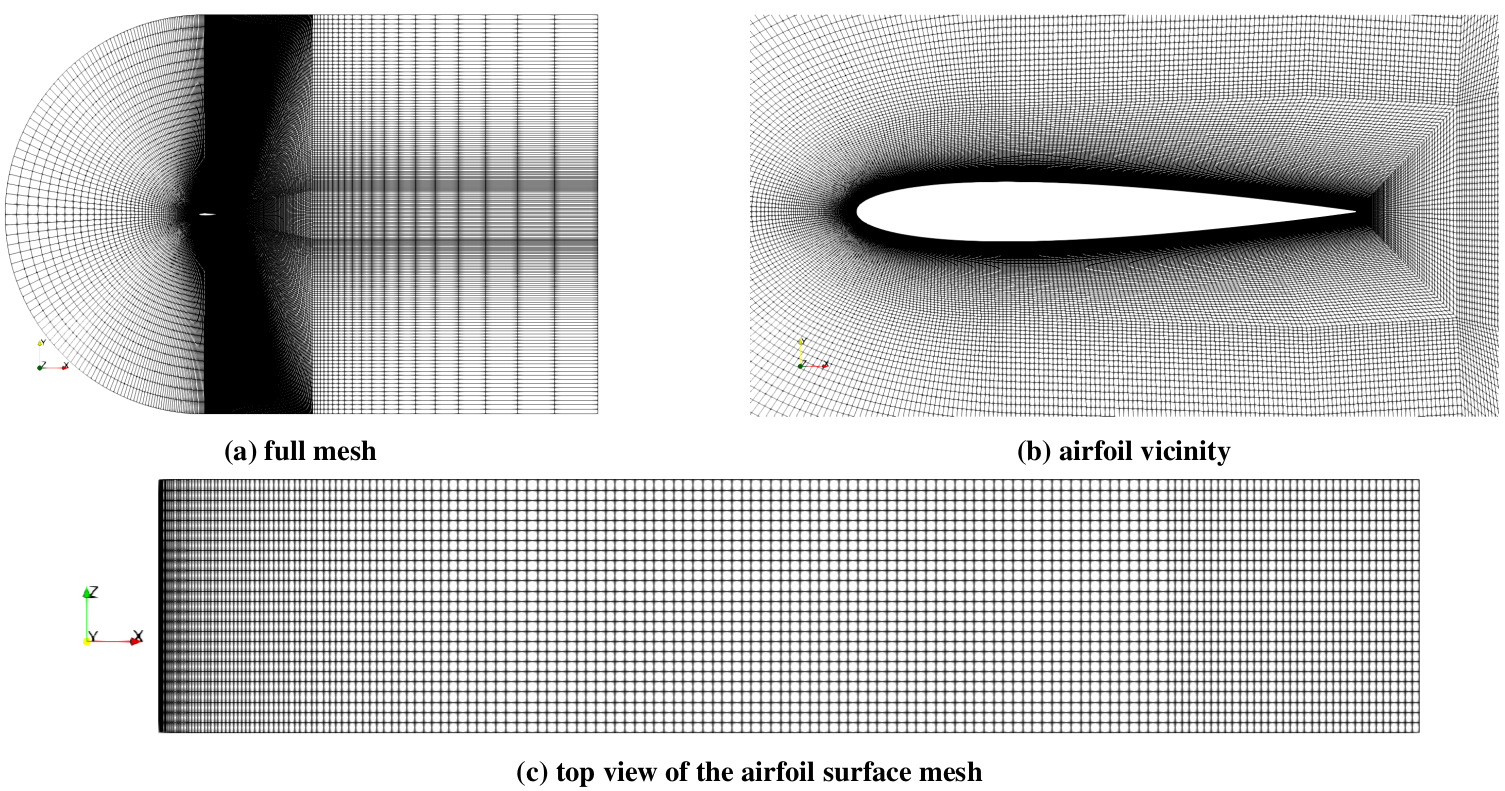
Various views of the computational mesh.

Dyanmic mode decomposition

Definition of data matrices:

$$ \mathbf{X} = \left[ \begin{array}{cccc} | & | & & | \\ \mathbf{x}_1 & \mathbf{x}_2 & ... & \mathbf{x}_{N-1} \\ | & | & & | \\ \end{array}\right],\quad \mathbf{X}^\prime = \left[ \begin{array}{cccc} | & | & & | \\ \mathbf{x}_2 & \mathbf{x}_3 & ... & \mathbf{x}_{N} \\ | & | & & | \\ \end{array}\right] $$

$\mathbf{x}_n$ - state vector snapshot at timestep $n$

DMD in a nutshell:

1. $\mathbf{X}^\prime = \mathbf{A} \mathbf{X}$
2. $\mathbf{A} = \mathbf{\Phi\Lambda\Phi}^{-1}$
3. $\mathbf{\Phi}$ - DMD modes
4. $\mathbf{\Lambda}$ - yields freq., stability

Key difference to previous studies:

1. volume-weighted state vector
2. thermodynamic variables in state vector$^*$
   $$ \mathbf{x}_n = \left[ \mathbf{u}_n, \mathbf{v}_n,\mathbf{w}_n, 2\mathbf{a}_n/\left(\gamma -1\right) \right]^T $$

$^*$ Rowley et al. 2004; $\gamma$ - adiabatic index, $a$ - local speed of sound, $u/v/w$ - velocity components

Practical DMD details:

• about 250 snapshots per cycle
• >3 cycles
• $-1 \le x/c \le 3$; $-1 \le y/c \le 1$
• only slice at $\tilde{z}=0$
• flowTorch for data processing and DMD

Results

Setup motivated by exp. investigations of McDevitt and Okuno 1985:

• NACA-0012 airfoil
• $Re_\infty = 10^7$
• $Ma_\infty = 0.75$
• pre-onset: $\alpha = 2^\circ$
• post-onset: $\alpha = 4^\circ$

Pressure coefficient $c_p$ at pre-onset conditions, $\alpha = 2^\circ$.

Pressure coefficient $c_p$ at post-onset conditions, $\alpha = 4^\circ$.

Local Mach number $Ma$, 2D, $\alpha=4^\circ$.

Slice of local Mach number $Ma$, 3D, $\alpha=4^\circ$.

DMD spectrum for 2D and 3D datasets/simulations; $\bar{f}=2\pi c f/U_\infty$.

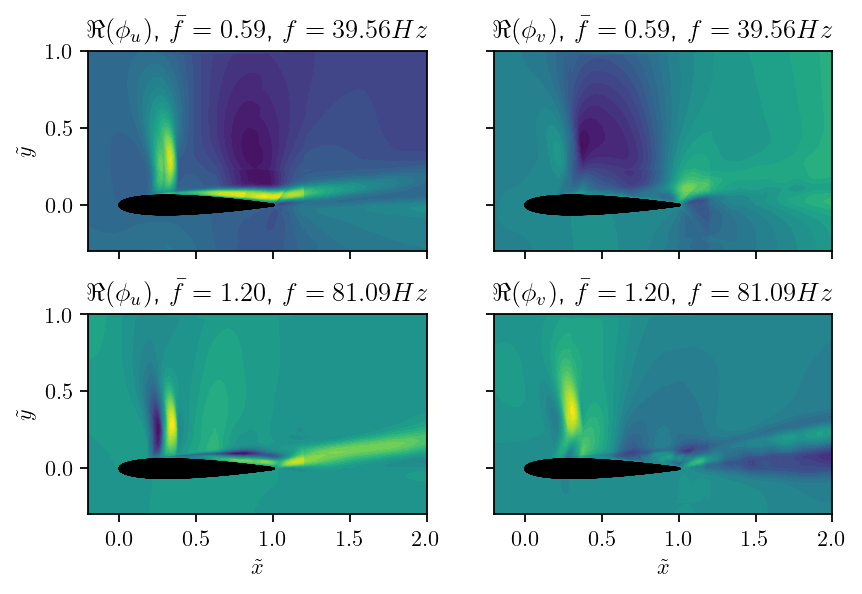
Real parts of DMD buffet mode and first harmonic; $u$ and $v$ are the velocity components.

DMD mode at approx. $20f_{buffet}$, $u$-component.

Summary and outlook

Summary

• 3D simulations yield more realistic results
• volume-weighted state vector
• thermodynamic variables in state vector
• workflow and data publicly available
• further 3D investigations

https://github.com/AndreWeiner/naca0012_shock_buffet

THE END

Thank you for you attention!

{a.weiner|r.semaan}@tu-braunschweig.de