simple and unified access to data

balance between flexibility and usability

full transparency - no need to reinvent the wheel

flowTorch overview

• development since July 2020
• Python, open-source (GPL-v3)
• uses PyTorch for data structures,
  linear algebra, machine learning, ...
• interface to common data formats
  TAU, OpenFOAM, VTK, CSV, iPSP,...

https://github.com/AndreWeiner/flowtorch

flowTorch packages

other content of the development repository

• simulation setups
• documentation
• tutorials

Jupyter labs

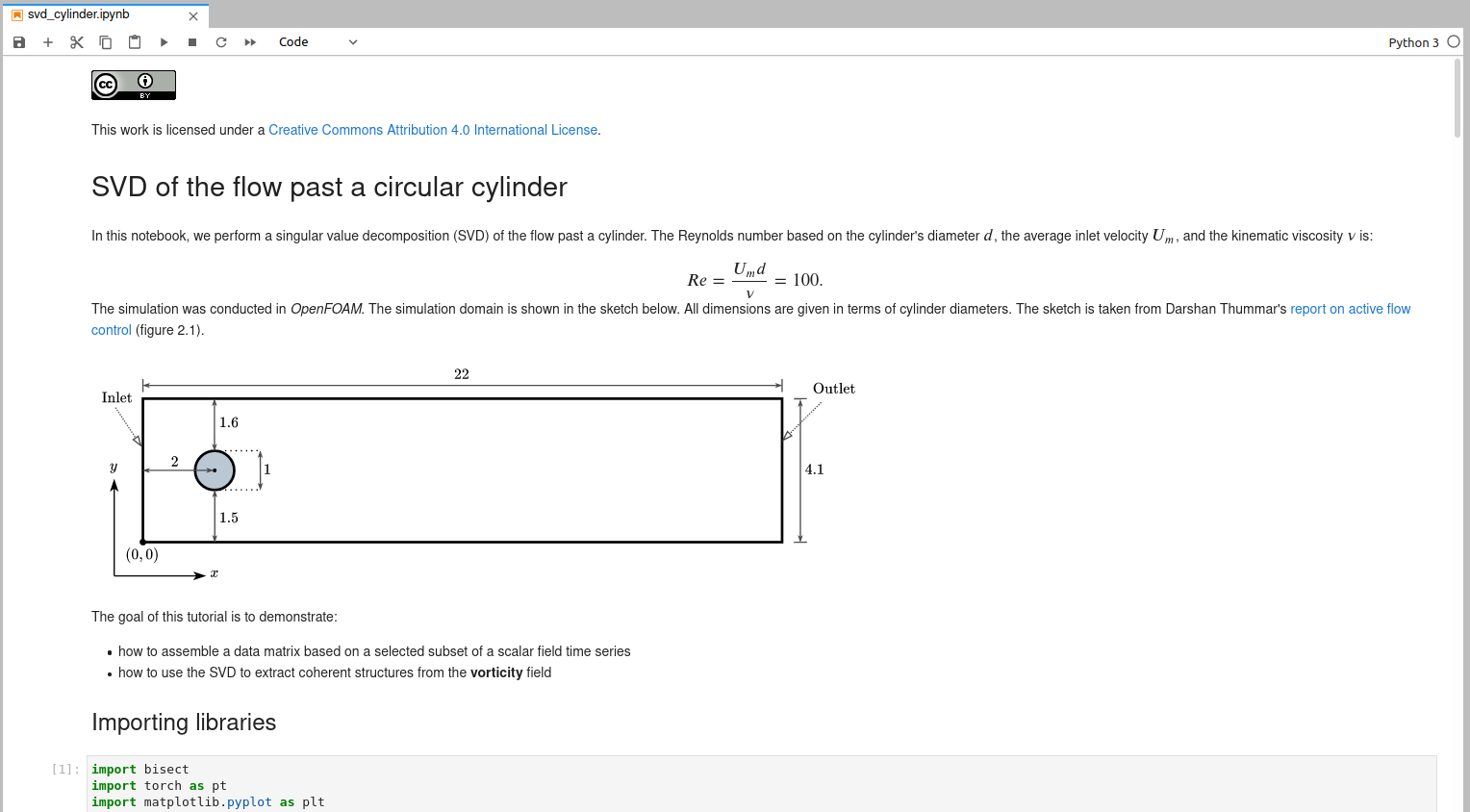
Analysis 1 - flow past a circular cylinder

2D OpenFOAM simulation; $Re=\bar{U}_{in}d/\nu = 100$; cylinder placed $0.1d$ off-center.

The goal

get a feeling for the flowTorch workflow

0. Importing modules

import torch as pt
from flowtorch import DATASETS
from flowtorch.data import FOAMDataloader, mask_box
from flowtorch.analysis import SVD
					

1. Create access, inspect available data

path = DATASETS["of_cylinder2D_binary"]
loader = FOAMDataloader(path)
times = loader.write_times
fields = loader.field_names
					

Number of available snapshots: 401
First five write times: ['0', '0.025', '0.05', '0.075', '0.1']
Fields available at t=10: ['p', 'vorticity', 'phi', 'U']

2. Create a mask

# load vertices and discard z-coordinate
vertices = loader.vertices[:, :2]
mask = mask_box(vertices, lower=[0.1, -1], upper=[0.75, 1])
					

Selected vertices: 7190/13678

3. Load the data and apply the mask

# select time window
window_times = [time for time in times if float(time) >= 4.0]
# allocate data matrix
data_matrix = pt.zeros((mask.sum().item(), len(window_times)))
# fill the data matrix
for i, time in enumerate(window_times):
    # load the vorticity vector field, take the z-component [:, 2]
    vorticity = loader.load_snapshot("vorticity", time)[:, 2]
    # apply mask
    data_matrix[:, i] = pt.masked_select(vorticity, mask)
    
# subtract the temporal mean from each snapshot
data_matrix -= pt.mean(data_matrix, dim=1).unsqueeze(-1)
					

4. Perform analysis - singular value decomposition (SVD/POD)

svd = SVD(data_matrix, rank=400)
print(svd)
					

SVD of a 7190x241 data matrix
Selected/optimal rank: 241/97
data type: torch.float32 (4b)
truncated SVD size: 6.8326Mb

5.1 Visualization - singular values

5.2 Visualization - POD modes (left singular vectors)

5.3 Visualization - POD mode coefficients

Analysis 2 - NACA 0012 transonic shock buffet

Transonic buffet on a NACA 0012 airfoil at Reynolds number $Re=10^7$, Mach number $Ma=0.75$, and angle of attack $\alpha=4^\circ$.

free buffet test data and setup

• experimental data by McDevitt & Okuno
• Naca 0012 airfoil, $Ma=0.75$, $Re=10^7$, $\alpha = 4^\circ$
• OpenFOAM, rhoPimpleFoam, 3D, SA-IDDES
• $f_{sim} = 28Hz$ (based on $c_L$),
  $f_{exp} = 31Hz$ (based on $c_p$)
• github.com/AndreWeiner/naca0012_shock_buffet

The goal

identify coherent structures associated with the buffet frequency

The tool

Dynamic Mode Decomposition (DMD)
typical goals of a DMD analysis include:

1. spectral analysis
2. stability analysis
3. reduced-order modeling

...
4. Perform analysis - dynamic mode decomposition

from flowtorch.analysis import DMD
# snip
dt = times_num[1] - times_num[0]
dmd = DMD(data_matrix, dt, rank=200)
print(dmd)
					

SVD of a 13950x149 data matrix
Selected/optimal rank: 149/51
... LSQ:
Overall DMD size: 24.0429Mb

5.1 Visualization - DMD spectrum

5.2 Visualization - DMD modes

What's next?

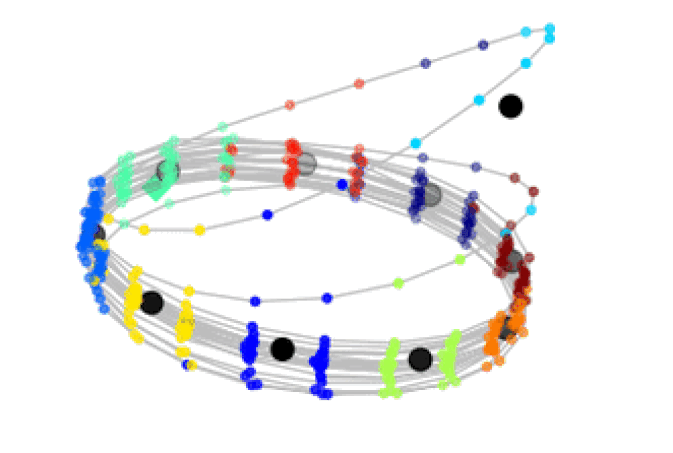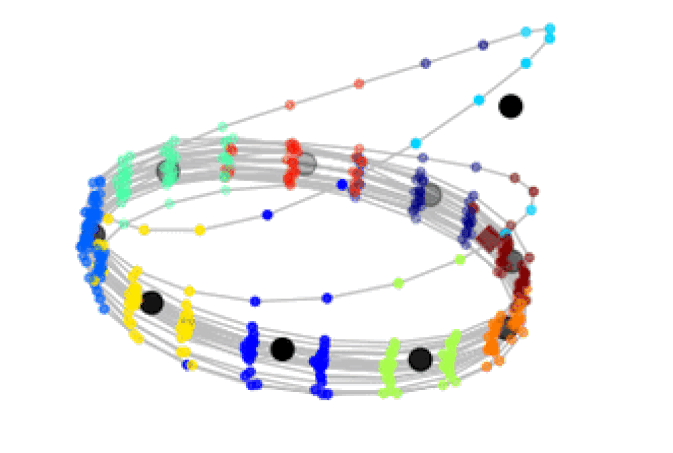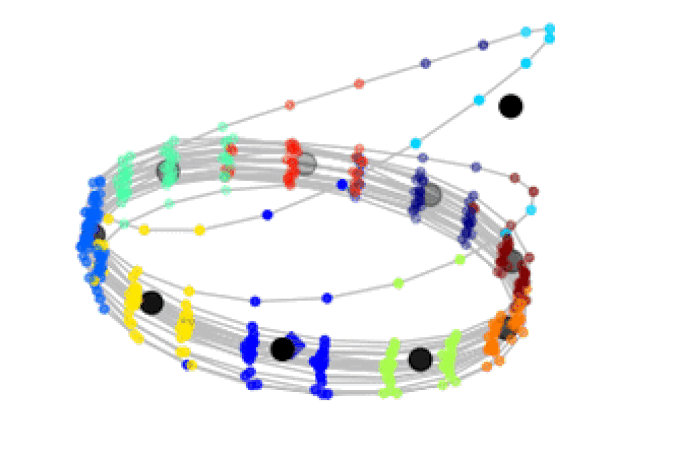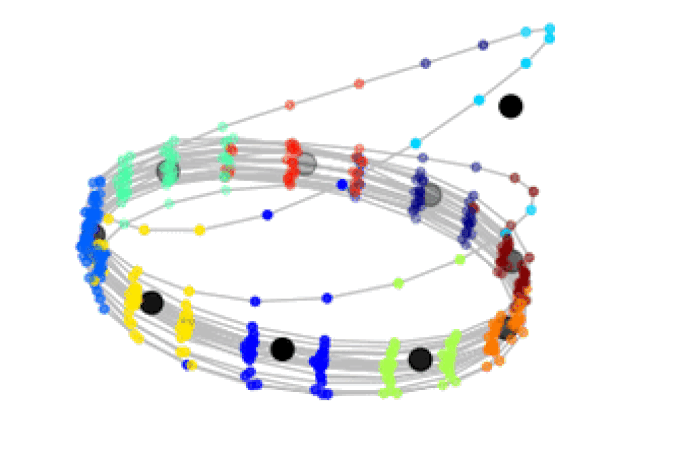
D. Fernex, B. R. Noack, R. Semaan:
Cluster-based network modeling - from snapshots to complex dynamical systems

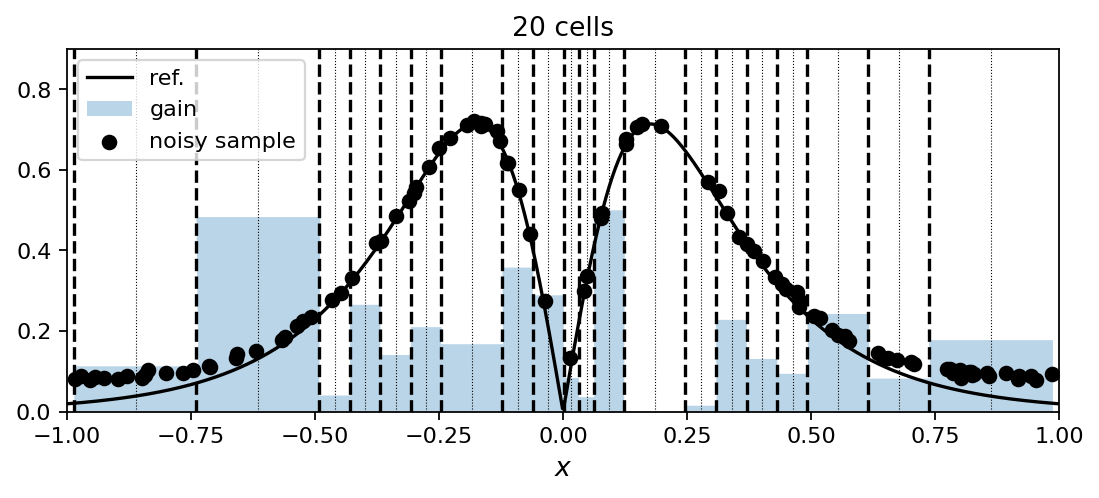
D. Fernex, A.Weiner, B. R. Noack, R. Semaan:
Sparse Spatial Sampling: a mesh sampling algorithm for efficient processing of big simulation data

Thank you for your attention!

Interested? github.com/AndreWeiner/flowtorch

{a.weiner|r.semaan}@tu-braunschweig.de