Reduced-order modeling for flow fields

Andre Weiner
TU Dresden, Institute of fluid mechanics, PSM Creative Commons License
These slides and most of the linked resources are licensed under a
Creative Commons Attribution 4.0 International License.

Last lecture(s)

Analyzing coherent structures in flows displaying transonic shock buffets

  • transonic shock buffet
  • principal component analysis (PCA)
  • ways to compute the PCA
  • dynamic mode decomposition (DMD)

Outline

Reduced-order modeling of flow fields

  • reduced-order models for dynamical systems
  • optimized DMD
  • dealing with high-dimensional data

Reduced-order models for dynamical systems

What is a reduced-order model (ROM)?

  • mathematical model with reduced
    • computational complexity
    • dimensionality
  • approximation
  • often derived from data

ROMs for dynamical systems

$$ \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t} = F(\mathbf{x}(t), t, ...) $$

Definition of ROMs in this lecture:

  1. encoding: $\tilde{\mathbf{x}}_n = E(\mathbf{x}_n)$
  2. evolution: $\tilde{\mathbf{x}}_{n+1} \approx f(\tilde{\mathbf{x}}_n)$
  3. decoding: $\hat{\mathbf{x}}_n \approx E^{-1}(\tilde{\mathbf{x}}_n)$

$\mathbf{x}$ - full state, $\tilde{\mathbf{x}}$ - reduced state, $\hat{\mathbf{x}}$ - full state prediction

Data-driven ROMs:
ML for encoding/decoding and/or temporal evolution.

Criteria for good ROMs:

  • computationally efficient
  • interpretable states and dynamics
  • long-term stability

Optimized DMD

review of some DMD basics

  1. $\mathbf{x}_n$: state vector at time $t_n = n\Delta t$
  2. core idea: $ \mathbf{x}_{n+1}=\mathbf{A}\mathbf{x}_n $
  3. diagonalization: $\mathbf{A}=\mathbf{\Phi}\mathbf{\Lambda}\mathbf{\Phi}^{-1}$
  4. prediction: $\mathbf{x}_{n} = \mathbf{\Phi\Lambda}^{n-1}\mathbf{\Phi}^{-1}\mathbf{x}_1$

$\rightarrow$ once $\mathbf{A}$ is known, the state at any $t_n$ may be predicted based on a given initial state $\mathbf{x}_1$

reconstruction of the full dataset

$$ \underbrace{ \begin{bmatrix} x_{11} & \ldots & x_{1N}\\ \vdots & \ddots & \vdots\\ x_{M1} & \ldots & x_{MN} \end{bmatrix} }_{\mathbf{M}} \approx \underbrace{ \begin{bmatrix} \phi_{11} & \ldots & \phi_{1r}\\ \vdots & \ddots & \vdots\\ \phi_{M1} & \ldots & \phi_{Mr} \end{bmatrix} }_{\mathbf{\Phi}} \underbrace{ \begin{bmatrix} b_1& & \\ & \ddots & \\ & & b_r \end{bmatrix} }_{\mathbf{D_b}} \underbrace{ \begin{bmatrix} \lambda_{1}^0 & \ldots & \lambda_{1}^{N-1}\\ \vdots & & \vdots\\ \lambda_r^0 & \ldots & \lambda_r^{N-1} \end{bmatrix} }_{\mathbf{V_\lambda}} $$

with $\mathbf{b} = \mathbf{\Phi}^{-1}\mathbf{x}_1$, $M$ - length of $\mathbf{x}$, $N$ - number of snapshots, $r$ - truncation rank

regular DMD

$\mathbf{X} = \left[ \mathbf{x}_1, \ldots, \mathbf{x}_{N-1} \right]^T$
$\mathbf{Y} = \left[ \mathbf{x}_2, \ldots, \mathbf{x}_{N} \right]^T$

$$ \underset{\mathbf{A}}{\mathrm{argmin}}\left|\left| \mathbf{Y}-\mathbf{AX} \right|\right|_F $$

optimizedDMD

$\mathbf{\Phi_b}=\mathbf{\Phi}\mathbf{D_b}$
$\mathbf{M} = \left[ \mathbf{x}_1, \ldots, \mathbf{x}_{N} \right]^T$

$$ \underset{\mathbf{\lambda},\mathbf{\Phi}_\mathbf{b}}{\mathrm{argmin}}\left|\left| \mathbf{M}-\mathbf{\Phi}_\mathbf{b}\mathbf{V}_{\mathbf{\lambda}} \right|\right|_F $$

$\rightarrow$ "optDMD" problem is non-linear and non-convex

idea: borrow techniques from ML/DL

  • stochastic gradient descent
  • automatic differentiation
  • train-validation-split
  • early stopping

$\rightarrow$ refer to article for details

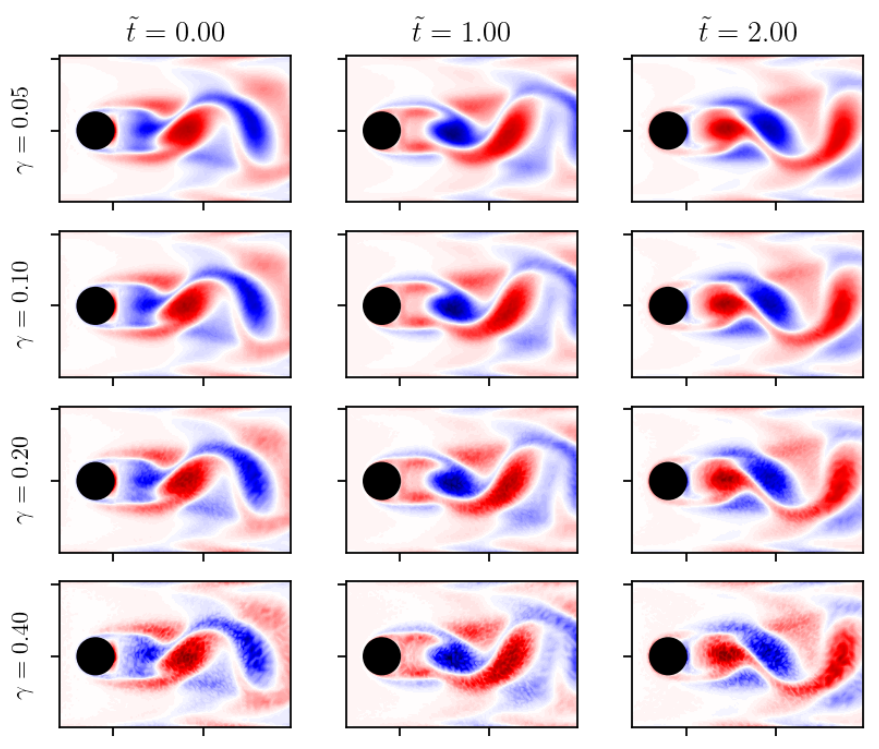
sh_glob

Test data with noise corruption.

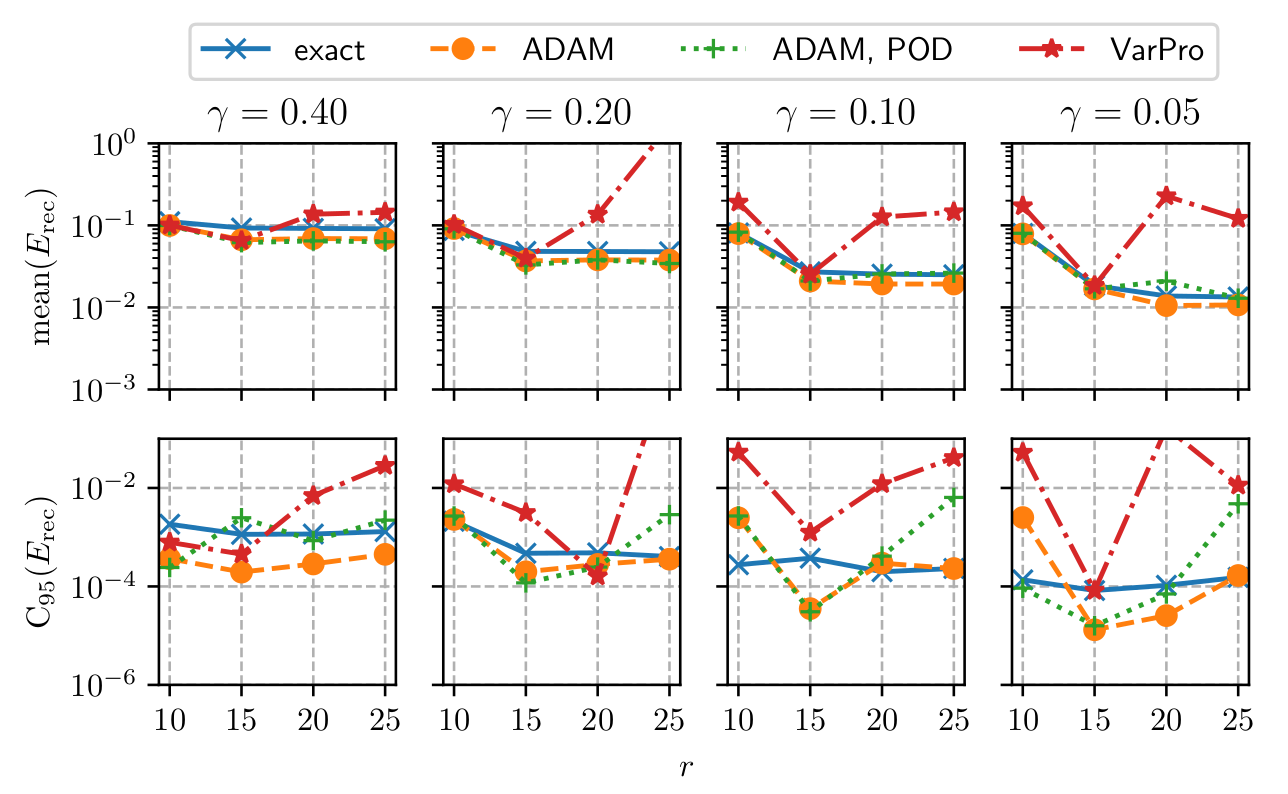
sh_glob

Comparison of DMD reconstruction error.

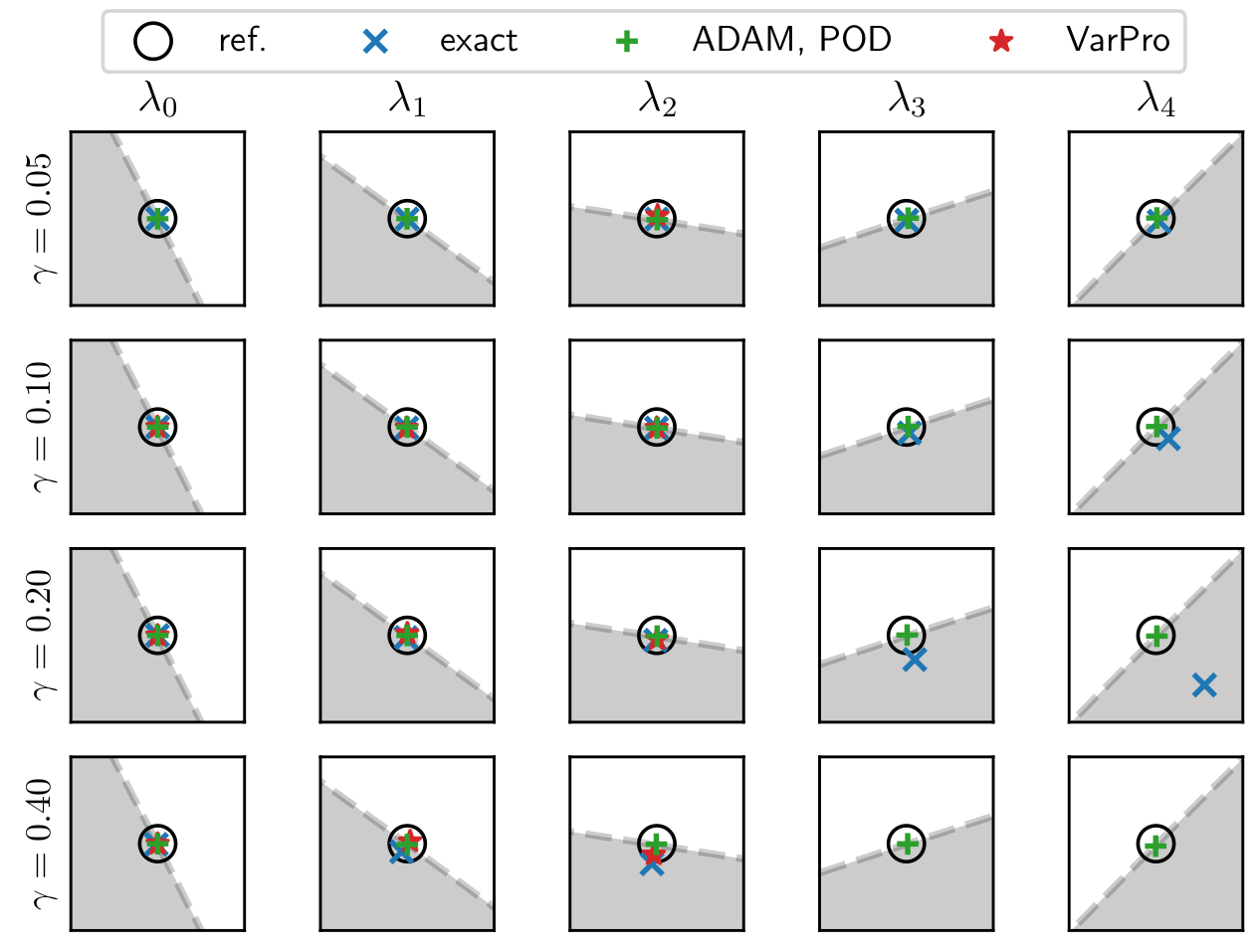
sh_glob

Comparison of dominant eigenvalues; reference computed with clean data.

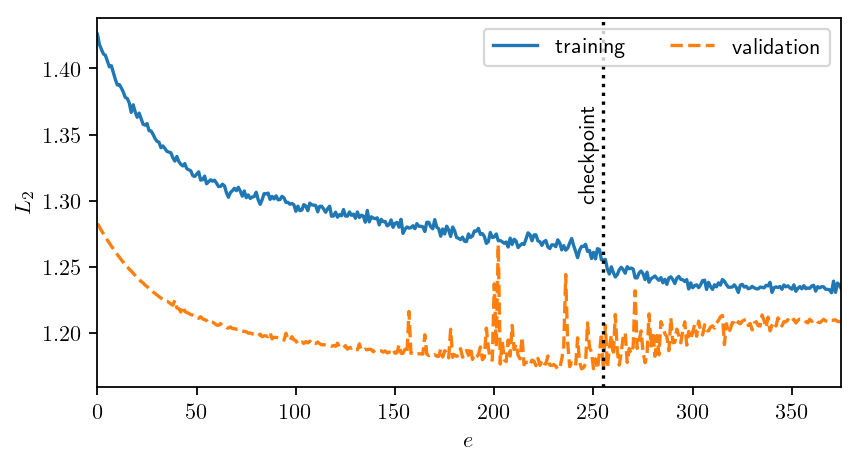
sh_glob

Early stopping prevents overfitting.

optimized DMD with sparsity promotion

$$ \underset{\mathbf{\lambda},\mathbf{\Phi}_\mathbf{b}}{\mathrm{argmin}}\left(\left|\left| \mathbf{M}-\mathbf{\Phi}_\mathbf{b}\mathbf{V}_{\mathbf{\lambda}} \right|\right|_F + \gamma_0 ||\mathbf{b}||_2\right) $$

$\rightarrow$ reduction to dominant dynamics

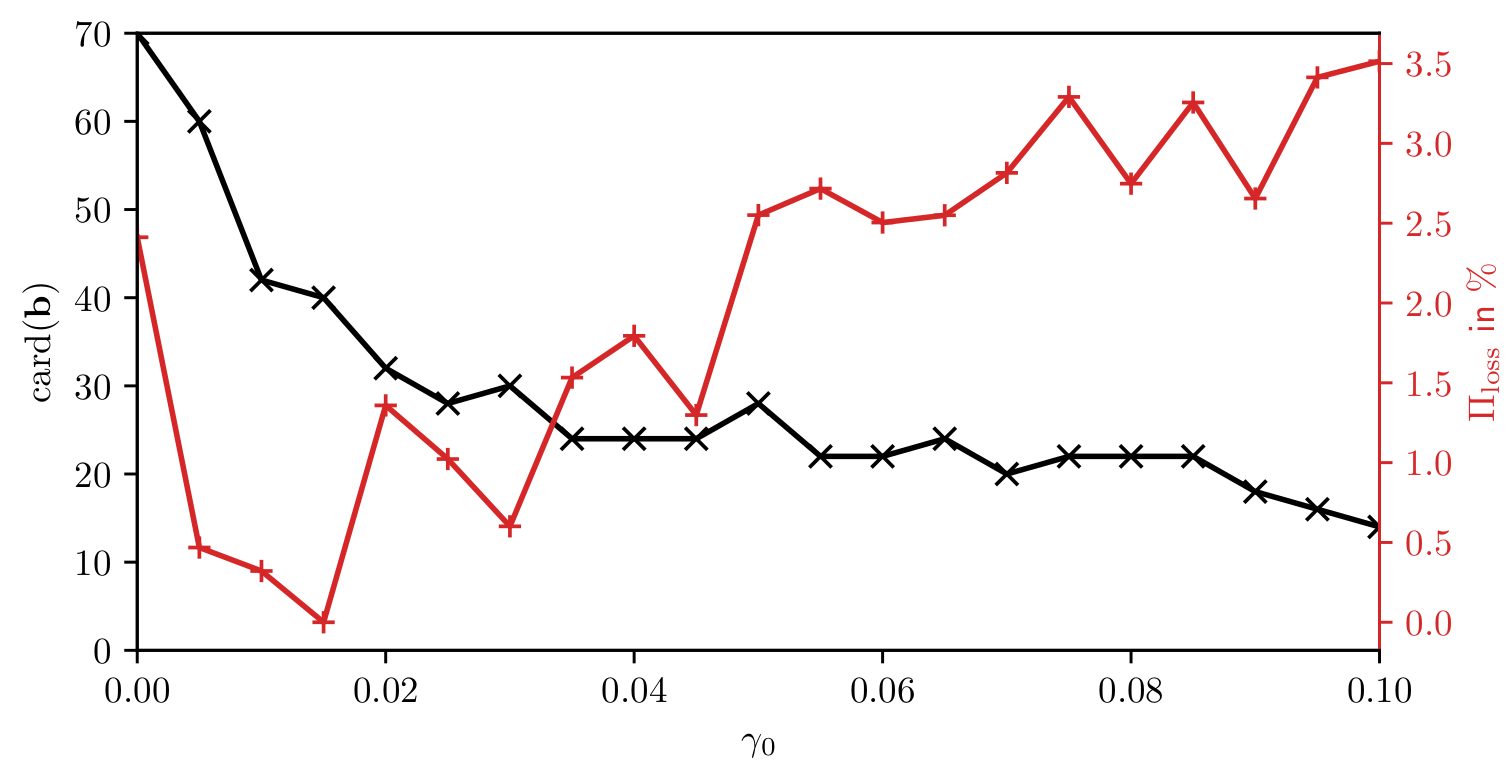
sh_glob

Cardinality of modes amplitudes and reconstruction error for increasing sparsity weight $\gamma_0$.

dealing with high-dimensional data

most common strategies

  1. project data on POD modes
  2. (variational) autoencoder
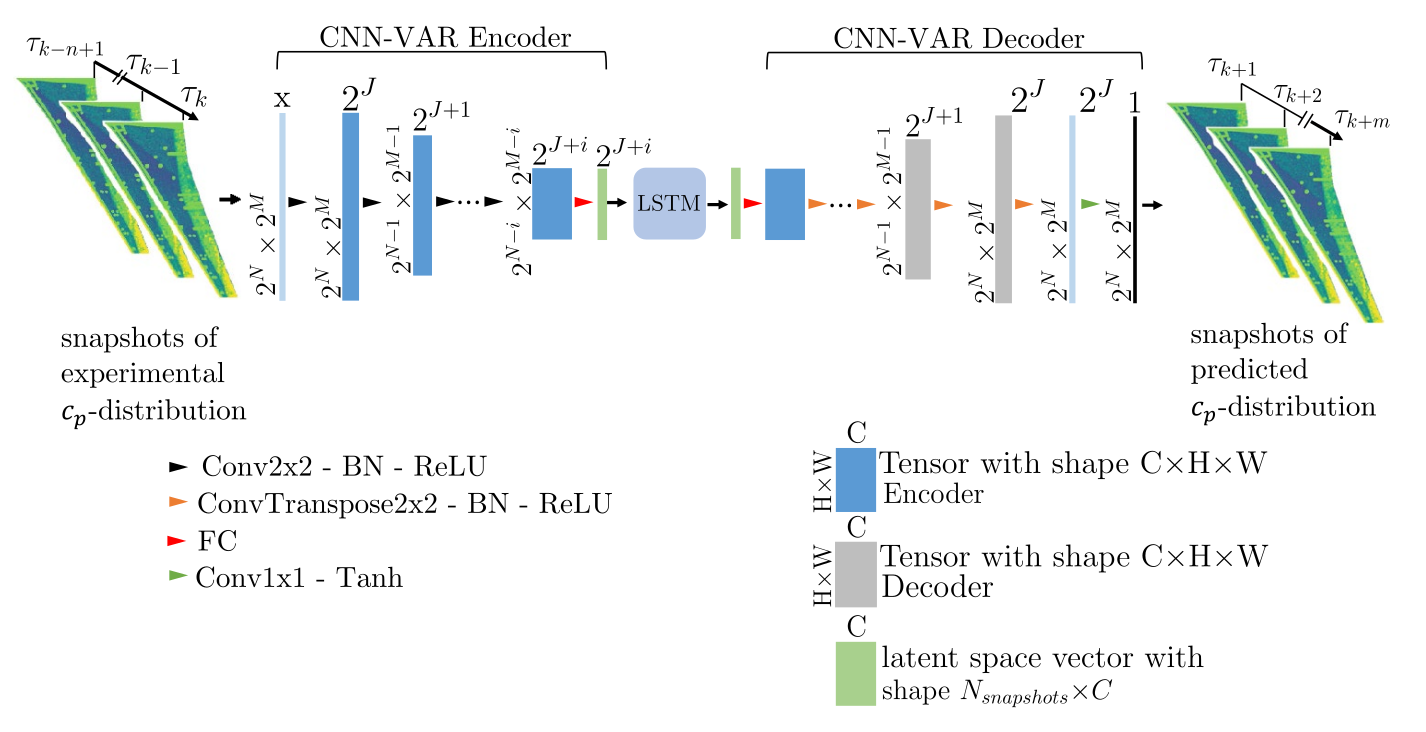
stencil

CNN-VAR-AE + LSTM; figure 2 from Zahn et al. (2023).